练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    观察下表：

    1，

    2,3，

    4,5,6,7，

    8,9,10,11,12,13,14,15，

    …，

    问：(1)此表第n行的最后一个数是多少？

    (2)此表第n行的各个数之和是多少？

    (3)2 013是第几行的第几个数？


    解　(1)∵第n＋1行的第1个数是2n，

    ∴第n行的最后一个数是2n－1.

    (2)2n－1＋(2n－1＋1)＋(2n－1＋2)…＋(2n－1)

    ＝＝3·22n－3－2n－2.

    (3)∵210＝1 024,211＝2 048,1 024<2 013<2 048，

    ∴2 013在第11行，该行第1个数是210＝1 024，

    由2 013－1 024＋1＝990，知2 013是第11行的第990个数．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    下面是关于公差d>0的等差数列{an}的四个命题：

    p1：数列{an}是递增数列；

    p2：数列{nan}是递增数列；

    p3：数列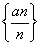是递增数列；

    p4：数列{an＋3nd}是递增数列．

    其中的真命题为(　　)

    A．p1，p2                                B．p3，p4

    C．p2，p3                                D．p1，p4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}的各项排成如图所示的三角形数阵，数阵中每一行的第一个数a1，a2，a4，a7，…构成等差数列{bn}，Sn是{bn}的前n项和，且b1＝a1＝1，S5＝15.

    a1

    a2　a3

    a4　a5　a6

    a7　a8　a9　a10

    …

    (1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列，且公比相等，已知a9＝16，求a50的值；

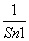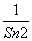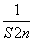    (2)设Tn＝＋＋…＋，求Tn.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若二次函数f(x)＝4x2－2(p－2)x－2p2－p＋1，在区间[－1,1]内至少存在一点c，使f(c)>0，则实数p的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于数25，规定第1次操作为23＋53＝133，第2次操作为13＋33＋33＝55，如此反复操作，则第2 011次操作后得到的数是(　　)

    A．25                                   B．250

    C．55                                   D．133

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(n)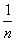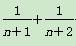＝＋＋…＋，则(　　)

    A．f(n)中共有n项，当n＝2时，f(2)＝＋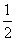

    B．f(n)中共有n＋1项，当n＝2时，f(2)＝＋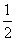

    C．f(n)中共有n2－n项，当n＝2时，f(2)＝＋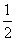

    D．f(n)中共有n2－n＋1项，当n＝2时，f(2)＝＋＋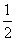

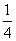
    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(n)＝12＋22＋32＋…＋(2n)2，则f(k＋1)与f(k)的递推关系是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若a>b>0，c<d<0，e<0.求证：

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若x，y∈(0,2]且xy＝2，使不等式a(2x＋y)≥(2－x)(4－y)恒成立，则实数a的取值范围为(　　)

    A．a≤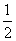                                B．a≤2

    C．a≥2                                 D．a≥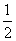

    查看答案和解析>>

    同步练习册答案