
已知f(n)=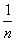 +
+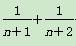 +…+
+…+ ,则( )
,则( )
A.f(n)中共有n项,当n=2时,f(2)=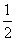 +
+
B.f(n)中共有n+1项,当n=2时,f(2)=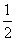 +
+
C.f(n)中共有n2-n项,当n=2时,f(2)=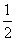 +
+
D.f(n)中共有n2-n+1项,当n=2时,f(2)=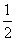 +
+ +
+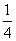
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
已知等比数列{an}满足an>0(n∈N*),且a5a2n-5=22n(n≥3),则当n≥1时,log2a1+log2a3+log2a5+…+log2a2n-1等于( )
A.(n+1)2 B.n2
C.n(2n-1) D.(n-1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题“设a,b为实数,则方程x3+ax+b=0至少有一个实根”时,要做的假设是( )
A.方程x3+ax+b=0没有实根
B.方程x3+ax+b=0至多有一个实根
C.方程x3+ax+b=0至多有两个实根
D.方程x3+ax+b=0恰好有两个实根
查看答案和解析>>
科目:高中数学 来源: 题型:
观察下表:
1,
2,3,
4,5,6,7,
8,9,10,11,12,13,14,15,
…,
问:(1)此表第n行的最后一个数是多少?
(2)此表第n行的各个数之和是多少?
(3)2 013是第几行的第几个数?
查看答案和解析>>
科目:高中数学 来源: 题型:
用数学归纳法证明34n+1+52n+1(n∈N*)能被8整除时,当n=k+1时,对于34(k+1)+1+52(k+1)+1可变形为( )
A.56·34k+1+25(34k+1+52k+1) B.34·34k+1+52·52k
C.34k+1+52k+1 D.25(34k+1+52k+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)设x≥1,y≥1,证明:x+y+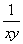 ≤
≤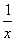 +
+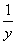 +xy;
+xy;
(2)设1<a≤b≤c,证明:logab+logbc+logca≤logba+logcb+logac.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com