练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知矩阵A=,向量α=.

    (1) 求A的逆矩阵;

    (2) 计算A5α的值.


     (1) 因为|A|==6≠0,

    故A-1==.

    (2) 矩阵A的特征多项式为f (λ)==λ2-5λ+6,

    由f(λ)=0,解得λ1=2,λ2=3.

    当λ1=2时,解得a1=;

    当λ2=3时,解得a2=,

    设α=ma1+na2,得解得m=3,n=1.

    则A5α=A5(3a1+a2)=3(A5a1)+A5a2=3(a1)+a2=3×25+35=.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     已知定义在R上的函数f(x)和g(x)满足g(x)≠0,f'(x)·g(x)<f(x)·g'(x),f(x)=ax·g(x),+=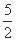.令an=,则使数列{an}的前n项和Sn超过的最小自然数n的值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正四棱柱ABCDA1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


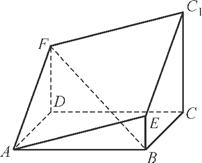
    如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.

    (1) 求BF的长;

     (2) 求点C到平面AEC1F的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若直线y=kx在矩阵对应的变换作用下得到的直线过点P(4,1),求实数k的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若双曲线x2-=1(a>0)的一个焦点到一条渐近线的距离等于,则此双曲线的方程为　　　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A,B两点,F为抛物线C的焦点,若FA=2FB,则k=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量a=(cosθ,sinθ),b=(,1),则|a-b|的最大值为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


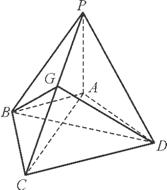
    如图,在四棱锥PABCD中,PA⊥平面ABCD,AB=BC=2,AD=CD=,PA=,∠ABC=120°,G为线段PC上的点.

    (1) 求证:BD⊥平面PAC;

    (2) 若PC⊥平面BGD,求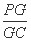的值.

    查看答案和解析>>

    同步练习册答案