练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在长为4cm的线段AB上任取一点C，现作一矩形，邻边长等于线段AC，CB的长，则矩形面积小于3cm2的概率为$\frac{1}{2}$．

    分析 设AC=x，则BC=4-x，求出对应矩形的面积，根据几何概型的概率公式进行计算即可．

    解答 解：设AC=x，则BC=4-x
    矩形的面积S=x（4-x），
    由S=x（4-x）＜3
    得x2-4x+3＞0
    ∴x＞3或x＜1，
    ∵0＜x＜4，
    ∴0＜x＜1或3＜x＜4
    由几何概率的求解公式可得，矩形面积小于3cm2的概率P=$\frac{1+1}{4}$=$\frac{1}{2}$．
    故答案为：$\frac{1}{2}$．

    点评 本题主要考查几何概型的概率的计算，利用条件求出矩形面积面积小于3cm2的等价条件是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．在直角坐标系中，曲线C的参数方程为，$\left\{\begin{array}{l}{x=\sqrt{5}cosφ}\\{y=\sqrt{15}sinφ}\end{array}\right.$（ϕ为参数），直线l的参数方程为$\left\{\begin{array}{l}{x=-\frac{1}{2}t}\\{y=\sqrt{3}+\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数）．以原点为极点，x轴的正半轴为极轴建立极坐标系，点P的极坐标为$（\sqrt{3}，\frac{π}{2}）$．
    （Ⅰ）求点P的直角坐标，并求曲线C的普通方程；
    （Ⅱ）设直线l与曲线C的两个交点为A，B，求|PA|+|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若圆C：x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称，则点（a，b）于圆心C之间的最小距离是（　　）
    A．$\sqrt{2}$B．2$\sqrt{2}$C．3$\sqrt{2}$D．4$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．如图是某市举办青少年运动会上，7位裁判为某武术队员打出的分数的茎叶图，左边数字表示十位数字，右边数字表示个位数字，这些数据的中位数是（　　），去掉一个最低分和最高分所剩数据的平均数是（　　）
    A．86.5，86.7B．88，86.7C．88，86.8D．86，5，86.8

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示，x1，x2分别表示知甲、乙两名同学这项测试成绩的众数，s12，s22分别表示知甲、乙两名同学这项测试成绩的方差，则有（　　）
    A．x1＞x2，s12＜s22B．x1=x2，s12＞s22C．x1=x2，s12=s22D．x1=x2，s12＜s22

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

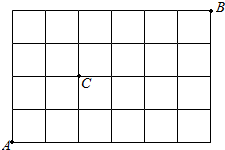
    8．如图，某地区有7条南北向街道，5条东西街道，从A点走向B点最短的走法中，必须经过C点的概率（　　）
    A．$\frac{3}{7}$B．$\frac{6}{7}$C．$\frac{3}{10}$D．$\frac{7}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在长方体ABCD-A1B1C1D1中，$\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{D{D_1}}$=（　　）
    A．$\overrightarrow{{D_1}{B_1}}$B．$\overrightarrow{{D_1}B}$C．$\overrightarrow{D{B_1}}$D．$\overrightarrow{B{D_1}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．命题“若x＞2，则x2+x＞6”的逆否命题是（　　）
    A．若x＞2，则x2+x≤6B．若x2+x≤6，则x≤2C．若x2+x＜6，则x＜2D．若x≤2，则x2+x≤6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

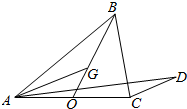    13．如图，在△ABC中，BO为边AC上的中线，$\overrightarrow{BG}=2\overrightarrow{GO}$，设$\overrightarrow{CD}$∥$\overrightarrow{AG}$，若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$（λ∈R），则λ的值为（　　）
    A．$\frac{1}{5}$B．$\frac{1}{2}$C．$\frac{6}{5}$D．2

    查看答案和解析>>

    同步练习册答案