Question

8．如图，某地区有7条南北向街道，5条东西街道，从A点走向B点最短的走法中，必须经过C点的概率（　　）

• A． $\frac{3}{7}$
• B． $\frac{6}{7}$
• C． $\frac{3}{10}$
• D． $\frac{7}{10}$

Answer 1

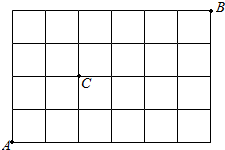
分析 先求出从A到B最短的走法的种数，再求出从A点走向B点最短的走法中，必须经过C点的走法种数，由此能求出从A点走向B点最短的走法中，必须经过C点的概率．

解答 解：10条街道分成6段，每条南北向街道被分成4段，
从A到B最短的走法，无论怎样走，一定包括10段，其中6段方向相同，另4段方向也相同，
每条走法，即是从10段中选出6条，这6段是东西方向的（剩下4段即是走南北方向的），
共有${C}_{10}^{6}$=${C}_{10}^{4}$=210种，
从A点走向B点最短的走法中，必须经过C点，
先从A到C，最短走法有C${\;}_{4}^{2}$=6种，从C到B，最短走法有${C}_{6}^{4}$=15种，
∴从A点走向B点最短的走法中，必须经过C点的概率P=$\frac{{C}_{4}^{2}•{C}_{6}^{4}}{{C}_{10}^{6}}$=$\frac{3}{7}$．
故选：A．

点评 本题考查概率的求法，是中档题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．