已知函数f(x)=10x,且实数a,b,c满足f(a)+f(b)=f(a+b),f(a)+f(b)+f(c)=f(a+b+c),则c的最大值为 .
【答案】
分析:由已知中函数f(x)=10
x,且实数a,b,c满足f(a)+f(b)=f(a+b),可得10
-a+10
-b=1,由基本不等式可得10
-(a+b)≤

,再由f(a)+f(b)+f(c)=f(a+b+c),可得10
-c≥

,进而可得c的最大值
解答:解:∵f(x)=10
x,f(a)+f(b)=f(a+b),
∴10
a+10
b=10
a+b=10
a×10
b…①
∴10
-a+10
-b=1.
由基本不等式可得10
-(a+b)≤

又∵f(a)+f(b)+f(c)=f(a+b+c),
∴10
a+10
b+10
c=10
a+b+c=10
a×10
b×10
c…②
将①代入②得:10
a×10
b+10
c=10
a×10
b×10
c
∴10
-c+10
-(a+b)=1,
∴10
-c≥

∴-c≥lg

∴c≤-lg

=
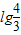
即c的最大值为
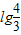
故答案为:
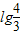 点评:
点评:本题考查的知识点是指数的运算性质,对数的运算性质,及基本不等式,其中根据已知结合基本不等式求出10
-a+10
-b=1进而得到10
-(a+b)≤

是解答的关键.

 ,再由f(a)+f(b)+f(c)=f(a+b+c),可得10-c≥
,再由f(a)+f(b)+f(c)=f(a+b+c),可得10-c≥ ,进而可得c的最大值
,进而可得c的最大值


 =
=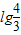
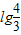
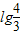
 是解答的关键.
是解答的关键. 

 名校课堂系列答案
名校课堂系列答案