
分析 (1)由题意可得:2bn=an+an+1,$a_{n+1}^2={b_n}•{b_{n+1}}$,由bn>0,an>0,$⇒2{(\sqrt{b_n})^2}=\sqrt{{b_{n-1}}{b_n}}+\sqrt{{b_n}{b_{n+1}}}(n≥2)$,可得$2\sqrt{b_n}=\sqrt{{b_{n-1}}}+\sqrt{{b_{n+1}}}$,即可证明,进而得出.
(2)利用“裂项求和”方法即可得出.
解答 (1)证明:由题意可得:2bn=an+an+1,$a_{n+1}^2={b_n}•{b_{n+1}}$,
∵a1=2,b1=4,∴a2=6,b2=9,
bn>0,an>0,an,bn,an+1成等差数列$⇒2{(\sqrt{b_n})^2}=\sqrt{{b_{n-1}}{b_n}}+\sqrt{{b_n}{b_{n+1}}}(n≥2)$,
∴$2\sqrt{b_n}=\sqrt{{b_{n-1}}}+\sqrt{{b_{n+1}}}$,
∴$\left\{{\sqrt{b_n}}\right\}$成等差数列,∴$\sqrt{b_n}=\sqrt{b_1}+(n-1)(\sqrt{b_2}-\sqrt{b_1})$$⇒{b_n}={(n+1)^2}$,
an=$\sqrt{{n}^{2}(n+1)^{2}}$=n(n+1).
(2)解:${c_n}=\frac{1}{{{{(n+1)}^2}-1}}=\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,
${S_n}=\frac{1}{2}(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n-1}-\frac{1}{n+1}+\frac{1}{n}-\frac{1}{n+2})$=$\frac{1}{2}(1+\frac{1}{2}-\frac{1}{n+1}-\frac{1}{n+2})=\frac{3}{4}-\frac{2n+3}{2(n+1)(n+2)}$.
点评 本题考查了递推关系、等差数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
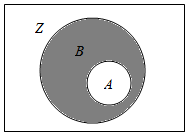 已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )
已知集合A={x∈Z|$\frac{x+1}{2-x}$≥0),B={x∈Z|-2<x≤3),则图中阴影部分表示的集合是( )| A. | {1,2,3) | B. | {2,3} | C. | {1,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
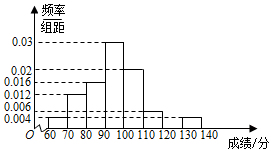 某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.
某校在一次期末考试中,全校学生的数学成绩都介于60分到140分之间(满分150分),为了估计该校学生的数学考试情况,从该校2000名学生的数学成绩中随机抽取50名学生的数学成绩,将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),…,第八组[130,140].如图是按照上述分组得到的频率分布直方图的一部分.估计该校2000名学生这次考试的数学成绩的平均分为97.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某房地产公司的新建小区有A,B两种户型住宅,其中A户型住宅的每套面积为100平方米,B户型住宅的每套面积为80平方米.该公司准备从两种户型中各拿出10套试销售,如表是这20套住宅每平方米的销售价格(单位:万元/平方米).
某房地产公司的新建小区有A,B两种户型住宅,其中A户型住宅的每套面积为100平方米,B户型住宅的每套面积为80平方米.该公司准备从两种户型中各拿出10套试销售,如表是这20套住宅每平方米的销售价格(单位:万元/平方米).| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| A户型 | 0.7 | 1.3 | 1.1 | 1.4 | 1.1 | 0.9 | 0.8 | 0.8 | 1.3 | 0.9 |
| B户型 | 1.2 | 1.6 | 2.3 | 1.8 | 1.4 | 2.1 | 1.4 | 1.2 | 1.7 | 1.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com