
分析 利用分析法结合等差数列的性质,三角形内角和定理,余弦定理即可证明.
解答 证明:要证$\frac{1}{a+b}+\frac{1}{b+c}=\frac{3}{a+b+c}$,
只需证(b+c)(a+b+c)+(a+b)(a+b+c)=3(a+b)(b+c),
即只需证a2-b2+c2-ac=0,①
又在△ABC中,角A、B、C的度数成等差数列,
有B=60°,则cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
即a2-b2+c2-ac=0,即 ①式显然成立,从而得证.
点评 本题主要考查了等差数列的性质,三角形内角和定理,余弦定理在解三角形中的综合应用,分析法是由未知探需知,逐步推向已知,属于中档题.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:选择题
| A. | 负 | B. | 正 | C. | 零 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<b<a | B. | 0<a<b | C. | a=b | D. | a≤b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证:
在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABCF是BC的中点,AB=AC=BE=2,CD=1.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$-$\frac{{\sqrt{2}}}{3}$i | B. | -$\frac{2}{3}$-$\frac{\sqrt{2}}{3}$i | C. | $\frac{2}{3}$+$\frac{\sqrt{2}}{3}$i | D. | -$\frac{2}{3}$+$\frac{\sqrt{2}}{3}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | lg2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
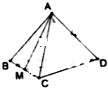 在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②
在四面体A-BCD中,棱长为4,M是BC的中点,点P在线段AM上运动,(点P不与A,M重合),过点P做直线l⊥平面ABC,l与平面BCD交于点Q.给出下列命题,其中正确的是①②查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com