
分析 (1)由已知利用向量共线的性质可得$\sqrt{3}$a=2csinA利用正弦定理化简可得$sinC=\frac{{\sqrt{3}}}{2}$,结合C为锐角,即可得解C的值.
(2)利用三角形面积公式可求ab=8,由余弦定理得(a+b)2-3ab=25,进而可求a+b的值,即可得解△ABC的周长.
解答 (本题满分为12分)
解:(1)由∵向量$\overrightarrow m=(2sinA,\sqrt{3}),\;\;\overrightarrow n=(a,c)$,且$\overrightarrow m∥\overrightarrow n$,
∴$\sqrt{3}$a=2csinA,---------------------------------------------2分
∴得:$\sqrt{3}$sinA=2sinCsinA,
∵sinA≠0,
∴$\sqrt{3}=2sinC$
∴$sinC=\frac{{\sqrt{3}}}{2}$
∴$C=\frac{π}{3}$(C为锐角).------6分
(2)∵S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$ab×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴ab=8,-------------------7分
由余弦定理得:a2+b2-2abcosC=c2,----------------------------8分
即:a2+b2-ab=25,(a+b)2-3ab=25,------------------------10分
∴(a+b)2=49,可得:a+b=7,
∴△ABC的周长为a+b+c=12.--------------------------------------------------12分.
点评 本题主要考查了平面向量共线的性质,正弦定理,三角形面积公式,余弦定理在解三角形中的综合应用,考查了转化思想的应用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 31 | C. | 33 | D. | 36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
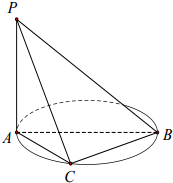 如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上异于A、B的点.
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上异于A、B的点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
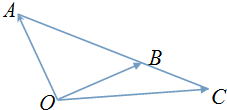
| A. | $\overrightarrow{c}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | B. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{c}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$ | D. | $\overrightarrow{c}$=$\overrightarrow{a}$+2$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com