Question

2．已知抛物线y²=4x上一点P在y轴上的射影为N，动点M在直线y=x+2上，则PM+PN的最小值为$\frac{3\sqrt{2}-2}{2}$．

Answer 1

分析 通过作抛物线的准线x=-1，过点P作x轴平行线交y轴、准线分别为N、Q点，通过抛物线定义可知PM+PN的最小值即为PF+PM-1的最小值即为抛物线焦点到直线y=x+2的距离减1，利用点到直线的距离计算即得结论．

解答 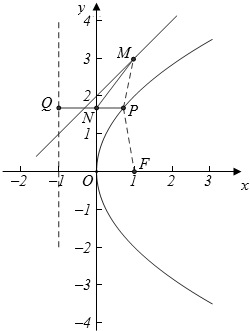解：依题意，作抛物线的准线x=-1，过点P作x轴平行线交y轴、准线分别为N、Q点，
记抛物线焦点F（1，0），连结PF、PM，
则点F到直线y=x+2的距离d=$\frac{|1-0+2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$，
由抛物线定义可知PF=PN+QN=PN+1，
于是PM+PN的最小值即为PF+PM-1的最小值，
通过图象可知PF+PM的最小值为d，
∴PM+PN的最小值为$\frac{3\sqrt{2}}{2}$-1=$\frac{3\sqrt{2}-2}{2}$，
故答案为：$\frac{3\sqrt{2}-2}{2}$．

点评 本题考查直线与圆锥曲线的关系，考查数形结合能力，注意解题方法的积累，属于中档题．