
分析 (1)先求出A、B的纵坐标,利用任意角的三角函数的定义求出tanα和 tanβ,再利用两角和的正切公式求得tan(α+β)的值.
(2)先求出 tan2β,tan(α+2β)=1.由(1)可得α∈($\frac{π}{2}$,$\frac{2π}{3}$)、β∈($\frac{3π}{4}$,π),可得α+2β∈(2π,$\frac{8π}{3}$),从而求得 α+2β 的值.
解答 解:(1)平面直角坐标系xOy中,以Ox轴为始边作两个钝角α,β,它们的终边分别与单位圆相交于A,B两点,
已知A,B的横坐标分别为-$\frac{\sqrt{2}}{10}$,-$\frac{2\sqrt{5}}{5}$,则A,B的横坐标分别为$\sqrt{{1-(-\frac{\sqrt{2}}{10})}^{2}}$=$\frac{7\sqrt{2}}{10}$,$\sqrt{{1-(-\frac{2\sqrt{5}}{5})}^{2}}$=$\frac{\sqrt{5}}{5}$.
∴tanα=$\frac{\frac{7\sqrt{2}}{10}}{-\frac{\sqrt{2}}{10}}$=-7,tanβ=$\frac{\frac{\sqrt{5}}{5}}{-\frac{2\sqrt{5}}{5}}$=-$\frac{1}{2}$,∴tan(α+β)=$\frac{tanα+tanβ}{1-tanα•tanβ}$=-$\frac{5}{3}$.
(2)由于tan2β=$\frac{2tanβ}{1{-tan}^{2}β}$=-$\frac{4}{3}$,tan(α+2β)=$\frac{tanα+tan2β}{1-tanα•tan2β}$=1.由(1)可得α∈($\frac{π}{2}$,$\frac{2π}{3}$)、β∈($\frac{3π}{4}$,π),
故α+2β∈(2π,$\frac{8π}{3}$),∴α+2β=$\frac{9π}{4}$.
点评 本题主要考查任意角的三角函数的定义,两角和的正切公式、二倍角的正切公式的应用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
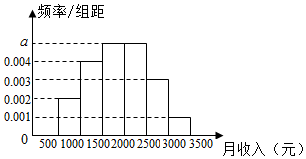 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com