练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．等比数列{an}前n和为sn，若s3+s6=s9，则q=±1．

    分析 对q分类讨论，利用等比数列的前n项和公式即可得出．

    解答 解：设等比数列{an}的公比为q，当q=1时，s3=3a1，s6=6a1，s9=9a1，满足s3+s6=s9，即q=1符合题意．
    当q≠1时，∵s3+s6=s9，∴$\frac{{a}_{1}（1-{q}^{3}）}{1-q}$+$\frac{{a}_{1}（1-{q}^{6}）}{1-q}$=$\frac{{a}_{1}（1-{q}^{9}）}{1-q}$，
    化为（1-q3）2（1+q3）=0，q≠1，解得q=-1．
    综上可得：q=±1．
    故答案为：±1．

    点评 本题考查了等比数列的前n项和公式，考查了分类讨论方法、推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．将函数y=cos2x的图象向左平移$\frac{π}{4}$个单位，得到函数y=f（x）•cosx的图象，则f（x）的表达式可以是（　　）
    A．f（x）=-2sinxB．f（x）=2sinx
    C．f（x）=$\frac{\sqrt{2}}{2}$sin2xD．f（x）=$\frac{\sqrt{2}}{2}$（sin2x+cos2x）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知f（x）=-x+sinx，命题p：?x∈（0，$\frac{π}{2}$），f（x）＜0，则（　　）
    A．p是假命题，￢p：?x∈（0，$\frac{π}{2}$），f（x）≥0B．p是假命题，￢p：?x0∈（0，$\frac{π}{2}$），f（x）≥0
    C．p是真命题，￢p：?x∈（0，$\frac{π}{2}$），f（x）≥0D．p是真命题，￢p：?x0∈（0，$\frac{π}{2}$），f（x）≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．解下列不等式：
    （1）4|3x-1|-1≤0；               
    （2）2|2x-1|＞1；
    （3）|x-1|+|x-3|≤4；              
    （4）|x+10|-|x-2|≥8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若$（{x^2}+\frac{1}{{\sqrt{x}}}{）^n}$的展开式中存在常数项，则n的一个可能取值是（　　）
    A．8B．9C．10D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．某地区有100户农民，都从事水产养殖．据了解，平均每户的年收入为3万元．为了调整产业结构，当地政府决定动员部分农民从事水产加工．据估计，如果能动员x（x＞0）户农民从事水产加工，那么剩下的继续从事水产养殖的农民平均每户的年收入有望提高2x%，而从事水产加工的农民平均每户的年收入将为$3（a-\frac{3x}{50}）（a＞0）$万元．
    （1）在动员x户农民从事水产加工后，要使从事水产养殖的农民的总年收入不低于动员前从事水产养殖的农民的总年收入，求x的取值范围；
    （2）若0＜x≤25，要使这100户农民中从事水产加工的农民的总年收入始终不高于从事水产养殖的农民的总年收入，求a的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

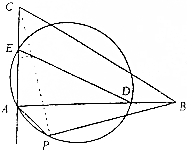    9．如图，△BC中，AB＞AC，点D、E分别在边AB、AC上，且BD=CE，∠BAC的外角平分线与△ADE的外接圆交于A、P两点．求证：A、P、B、C四点共圆．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．某学校高二学生进行研究性学习，某班共有m（m∈N*）名学生编号为1、2、3…m，有n（n∈N*）台设备编号分别为1、2、3…n，定义记号aij；如果第i名学生操作了第j台设备，此时规定aij=1否则aij=0，则等式a41+a42+a43+…a4n=3的实际意义为（　　）
    A．第4名学生操作了n台设备B．第4名学生操作了3台设备
    C．第3名学生操作了n台设备D．第3名学生操作了4台设备

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，连接椭圆四个顶点形成的四边形面积为4$\sqrt{2}$，求椭圆C的标准方程．

    查看答案和解析>>

    同步练习册答案