
【题目】已知等差数列{an}中,a1=1,且a1 , a2 , a4+2成等比数列.
(1)求数列{an}的通项公式及其前n项和Sn;
(2)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】
(1)解:设等差数列{an}的公差为d,∵a1=1,且a1,a2,a4+2成等比数列.
∴ ![]() =a1(a4+2),即(1+d)2=1×(1+3d+2),解得d=2或﹣1.
=a1(a4+2),即(1+d)2=1×(1+3d+2),解得d=2或﹣1.
其中d=﹣1时,a2=0,舍去.
∴d=2,可得an=1+2(n﹣1)=2n﹣1.
Sn= ![]() =n2.
=n2.
(2)解: ![]() =
= ![]() .
.
∴当n为偶数时, ![]() =
= ![]() =16.当n为奇数时,
=16.当n为奇数时, ![]() =
= ![]() =
= ![]() .
.
∴数列{bn}的奇数项是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.
为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.
∴数列{bn}的前2n项和T2n=(b1+b3+…+b2n﹣1)+(b2+b4+…+b2n)
= 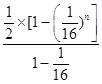 +
+ ![]()
= ![]() (16n﹣16﹣n).
(16n﹣16﹣n).
【解析】(1)设等差数列{an}的公差为d,由a1=1,且a1,a2,a4+2成等比数列.可得: ![]() =a1(a4+2),即(1+d)2=1×(1+3d+2),解得d.经过验证可得d,再利用等差数列的通项公式与求和公式即可得出.(2)
=a1(a4+2),即(1+d)2=1×(1+3d+2),解得d.经过验证可得d,再利用等差数列的通项公式与求和公式即可得出.(2) ![]() =
= ![]() .当n为偶数时,
.当n为偶数时, ![]() =
= ![]() =16.当n为奇数时,
=16.当n为奇数时, ![]() =
= ![]() =
= ![]() .可得数列{bn}的奇数项是以
.可得数列{bn}的奇数项是以 ![]() 为首项,
为首项, ![]() 为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.利用求和公式即可得出.
为公比的等比数列;偶数项是以8为首项,16为公比的等比数列.利用求和公式即可得出.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系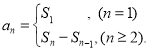 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论: ① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]()
其中正确的结论是: . (填上你认为所有正确的结论序号)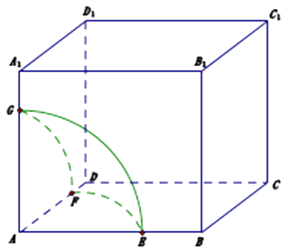
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ![]() ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120° 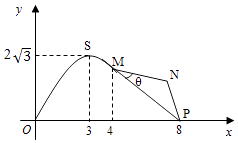
(1)求A,ω的值和M,P两点间的距离;
(2)应如何设计,才能使折线段赛道MNP最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(1)求证:BD⊥EG;
(2)求平面DEG与平面DEF所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数,且f(x+2)=f(x﹣2);当0≤x≤1时,f(x)= ![]() ,则f(1)+f(2)+f(3)+…+f等于( )
,则f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是
的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是 ![]() ,如图所示.
,如图所示.
(1)求椭圆的标准方程;
(2)抛物线的准线与椭圆在第二象限相交于点A,过点A作抛物线的切线l,l与椭圆的另一个交点为B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆 ![]() 为参数)上的每一点的横坐标保持不变,纵坐标变为原来的
为参数)上的每一点的横坐标保持不变,纵坐标变为原来的 ![]() 倍,得到曲线C.
倍,得到曲线C.
(1)求出C的普通方程;
(2)设直线l:x+2y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系, 求过线段P1P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com