
| A. | 命题“?x0∈R,x02+x0+1<0”的否定是:“?x∈R,x2+x+1>0.” | |
| B. | “x>0,y>0”是“$\frac{y}{x}+\frac{x}{y}≥2$”的充要条件 | |
| C. | 命题:“若sinx=siny则x=y”的逆否命题为真命题 | |
| D. | 数据1,3,2,4,3,5的平均数、众数、中位数都是3 |
分析 A.根据特称命题的否定是全称命题进行判断,
B.根据基本不等式成立的条件进行判断,
C.根据逆否命题的等价性进行判断,
D.求出平均数,众数和中位数进行判断.
解答 解:A.命题“?x0∈R,x02+x0+1<0”的否定是:“?x∈R,x2+x+1≥0”,故A错误,
B.当x>0,y>0时,$\frac{y}{x}+\frac{x}{y}≥2$$\sqrt{\frac{x}{y}•\frac{y}{x}}$=2成立,
当x<0,y<0时,满足$\frac{y}{x}+\frac{x}{y}≥2$$\sqrt{\frac{x}{y}•\frac{y}{x}}$=2成立,但x>0,y>0不成立,故B错误,
C.当x=$\frac{π}{4}$,y=$\frac{3π}{4}$时,满足sinx=siny,但x=y不成立,则原命题为假命题,则逆否命题也为假命题,故C错误,
D.数据1,3,2,4,3,5,即1,2,3,3,4,5,
则平均数为$\frac{1+2+3+3+4+5}{6}=\frac{18}{6}$=3.众数为3,中位数为3,则平均数、众数、中位数都是正确,故D正确,
故选:D
点评 本题主要考查命题的真假判断,涉及知识点较多,综合性较强,难度不大.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {3} | C. | {1,2,3,5} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
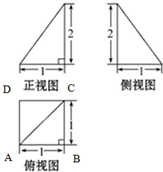 已知一四棱锥P-ABCD的三视图如图.
已知一四棱锥P-ABCD的三视图如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁U(∁UA)={A} | B. | 若A∩B=B,则A⊆B | ||
| C. | 若A={1,∅,{2}},则{2}?A | D. | 若A={1,2,3},B={x|x⊆A},则A∈B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-6,-10) | B. | (6,10) | C. | (-2,-4) | D. | (2,4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com