
【题目】已知圆心C(1,2),且经过点(0,1) (Ⅰ)写出圆C的标准方程;
(Ⅱ)过点P(2,﹣1)作圆C的切线,求切线的方程及切线的长.
【答案】解(Ⅰ)∵圆心C(1,2),且经过点(0,1) 圆C的半径 ![]() ,
,
∴圆C的标准方程:(x﹣1)2+(y﹣2)2=2,
(Ⅱ)设过点P(2,﹣1)的切线方程为y+1=k(x﹣2),
即kx﹣y﹣2k﹣1=0,有: ![]() ,
,
∴k2﹣6k﹣7=0,解得k=7或k=﹣1,
∴所求切线的方程为7x﹣y﹣15=0或x+y﹣1=0,
由圆的性质可知: ![]()
【解析】(Ⅰ)求出圆的半径,即可写出圆C的标准方程;(Ⅱ)利用点斜式设出过点P(2,﹣1)作圆C的切线方程,通过圆心到切线的距离等于半径,求出切线的斜率,然后求出方程,通过切线的长、半径以及圆心与P点的距离满足勾股定理,求出切线长.
【考点精析】关于本题考查的圆的标准方程,需要了解圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程才能得出正确答案.
;圆心为A(a,b),半径为r的圆的方程才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某学校对高三学生一次模拟考试的数学成绩进行分析,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.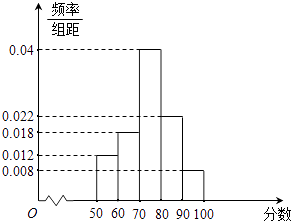
(1)根据频率分布直方图估计这次考试全校学生数学成绩的众数、中位数和平均值;
(2)若成绩不低于80分为优秀成绩,视频率为概率,从全校学生中有放回的任选3名学生,用变量ξ表示3名学生中获得优秀成绩的人数,求变量ξ的分布列及数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,2),B(﹣1,2),动点P满足 ![]() ,若双曲线
,若双曲线 ![]() =1(a>0,b>0)的渐近线与动点P的轨迹没有公共点,则双曲线离心率的取值范围是 .
=1(a>0,b>0)的渐近线与动点P的轨迹没有公共点,则双曲线离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ ![]() x+c(a,c∈R)满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0
x+c(a,c∈R)满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0
(1)求a、c的值;
(2)若存在实数m,使函数g(x)=f(x)﹣mx在区间[m,m+2]上有最小值﹣5,求出实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有大小相同的2个红球和6个白球的袋子中,每摸出2个球为一次试验,直到摸出的球中有红球(不放回),则试验结束.
(1)求第一次试验恰摸到一个红球和一个白球概率;
(2)记试验次数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com