
分析 因为方程|x+a|•2x=2013的根的个数,可以转化为对应函数图象交点的个数,所以可以借助于图形求解画出函数的图象即可得到答案..
解答 解:因为 方程|x+a|•2x=2013的根个数就是函数y=|x+a|,y=2013×2-x交点个数,画出对应图象得
①当a<0时即y=|x+a|的图象在y轴右侧,且离y轴很远时,交点有2个;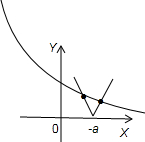
②当a>0并且比较大即y=|x+a|的图象在y轴左侧,且离y轴很远时,因为指数函数的递增递减较快,故交点有3个.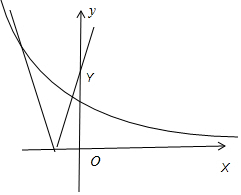
③当a>0比较小时,如图: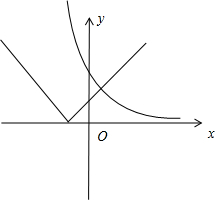
只有一个交点.
即集合A={1,2,3}
故答案为 {1,2,3}.
点评 本题主要考查根的个数判断问题.因为方程根的个数可以转化为对应函数图象的交点个数,所以通常借助与图形求解.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
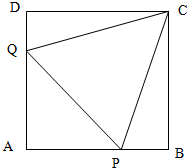 如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com