
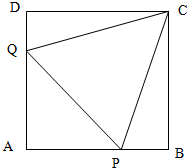
 如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.
如图,正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且都不与A,B,D重合,线段PQ的长为1,△CPQ的面积用y表示.分析 (1)由已知得|AP|=cosθ,|AQ|=sinθ,|BP|=1-cosθ|DQ|=1-sinθ,即可用y表示为θ的函数;
(2)令$cosθ+sinθ=\sqrt{2}sin(θ+\frac{π}{4})=t$,则1+2sinθcosθ=t2,得$sinθcosθ=\frac{{{t^2}-1}}{2}$,利用配方法求△CPQ的面积y的最小值.
解答 解:(1)由已知得|AP|=cosθ,|AQ|=sinθ,∴|BP|=1-cosθ|DQ|=1-sinθ.$y={S_{△CPQ}}=1-[{\frac{1}{2}sinθcosθ+\frac{1}{2}(1-cosθ)+\frac{1}{2}(1-sinθ)}]$…(2分)
=$1-[{\frac{1}{2}sinθcosθ-\frac{1}{2}(cosθ+sinθ)+1}]$
=$\frac{1}{2}(cosθ+sinθ-cosθsinθ)(0<θ<\frac{π}{2}$)…(4分).
(2)令$cosθ+sinθ=\sqrt{2}sin(θ+\frac{π}{4})=t$…(6分)
则1+2sinθcosθ=t2,得$sinθcosθ=\frac{{{t^2}-1}}{2}$,
∴$y=\frac{1}{2}(t-\frac{{{t^2}-1}}{2})=\frac{1}{2}(-\frac{1}{2}{t^2}+t+\frac{1}{2})$=$-\frac{1}{4}{({t-1})^2}+\frac{1}{2}$…(8分)
∵$0<θ<\frac{π}{2}$,∴$\frac{π}{4}<θ+\frac{π}{4}<\frac{3}{4}π$,
∴$\frac{{\sqrt{2}}}{2}<sin(θ+\frac{π}{4})≤1$,∴$1<t≤\sqrt{2}$…(10分)
∴${y_{min}}=\frac{{2\sqrt{2}-1}}{4}$…(12分)
点评 本题考查三角函数知识的运用,考查换元、配方法,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
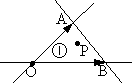 如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )
如图,已知O,A,B是平面内不共线的三点,且$\overrightarrow{OP}=x\overrightarrow{OA}+y\overrightarrow{OB}$,直线OA,OB,AB将平面区域分成7部分,若点P落在区域①中(含边界),则z=2x+y的最大值为( )| A. | 不存在 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)+f(-2)<2f(-$\frac{3}{2}$) | B. | f(-1)+f(-2)>2f(-$\frac{3}{2}$) | C. | f(-1)+f(-2)≤2f(-$\frac{3}{2}$) | D. | f(-1)+f(-2)≥2f(-$\frac{3}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com