Question

已知函数，如果函数恰有两个不同的极值点，，且.
（Ⅰ）证明：；（Ⅱ）求的最小值，并指出此时的值.

Answer 1

（Ⅰ）详见解析；（Ⅱ）最小值为，此时.

解析试题分析：（Ⅰ）函数有两个不同的极值点，等价于有两个不等的实数根，即有两个不同的零点和，利用导数判断的形状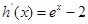， ，发现函数当时，是减函数；当时，是增函数，故；（Ⅱ），又，故，是自变量为，定义域的函数，利用导数求其最值，并计算相应的值．
试题解析：（Ⅰ）∵ 函数恰有两个不同的极值点，，即有两个零点，，
∴方程有两个不同的零点，， 令，，当时，，是减函数；当时，，是增函数，∴ 在时取得最小值．
∴ ．
（Ⅱ）∵，即，∴，于是
， ∴，∵，∴．
∴ 当时，，是减函数；当时，，是增函数．
∴ 在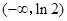上的最小值为，此时.
考点：1、导数在单调性上的应用；2、利用导数求函数的极值和最值.