
已知函数 ,其中
,其中 为常数.
为常数.
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若任取 ,求函数
,求函数 在
在 上是增函数的概率.
上是增函数的概率.
(Ⅰ)函数 的单调递增区间分别为
的单调递增区间分别为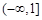 和
和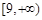 ;(Ⅱ)函数
;(Ⅱ)函数 在
在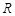 上是增函数的概率为
上是增函数的概率为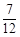 .
.
解析试题分析:(Ⅰ)求函数 的单调递增区间,首先将
的单调递增区间,首先将 代入,我们易求出函数的解析式,从而求出函数的导函数后,令导函数的函数值大于等于0,由此构造关于
代入,我们易求出函数的解析式,从而求出函数的导函数后,令导函数的函数值大于等于0,由此构造关于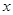 的不等式,解不等式即可得到函数
的不等式,解不等式即可得到函数 的单调递增区间;(Ⅱ)求函数
的单调递增区间;(Ⅱ)求函数 在
在 上是增函数的概率,这是一个几何概型问题,我们可以先画出
上是增函数的概率,这是一个几何概型问题,我们可以先画出 ,对应的平面区域的面积,然后再求出满足条件函数
,对应的平面区域的面积,然后再求出满足条件函数 在
在 上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
上是增函数时对应的平面区域的面积,计算出对应的面积后,代入几何概型公式即可得到答案.
试题解析:(1)当 时,
时, ,
,
令 ,
, ,解得
,解得 或
或 ,
,
故函数 的单调递增区间分别为
的单调递增区间分别为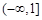 和
和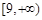
(2)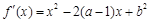
若函数 在
在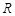 上是增函数,则对于任意
上是增函数,则对于任意 ,
,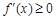 恒成立.
恒成立.
所以,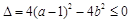 ,即
,即 8分
8分
设“ 在
在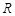 上是增函数”为事件
上是增函数”为事件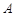 ,则事件
,则事件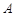 对应的区域为
对应的区域为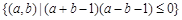
全部试验结果构成的区域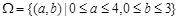 ,
,
所以,
故函数 在
在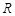 上是增函数的概率为
上是增函数的概率为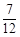
考点:利用导数研究函数的单调性;几何概型;概率的应用.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
已知a,b为常数,a¹0,函数 .
.
(1)若a=2,b=1,求 在(0,+∞)内的极值;
在(0,+∞)内的极值;
(2)①若a>0,b>0,求证: 在区间[1,2]上是增函数;
在区间[1,2]上是增函数;
②若 ,
, ,且
,且 在区间[1,2]上是增函数,求由所有点
在区间[1,2]上是增函数,求由所有点 形成的平面区域的面积.
形成的平面区域的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 =
= 。
。
(1)当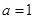 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)求函数 在区间
在区间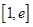 上的最小值;
上的最小值;
(3)在(1)的条件下,设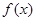 =
= +
+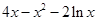 ,
,
求证: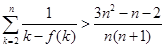 (
(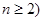 ),参考数据:
),参考数据: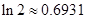 。(13分)
。(13分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知 .
.
(1)曲线y=f(x)在x=0处的切线恰与直线 垂直,求
垂直,求 的值;
的值;
(2)若x∈[a,2a]求f(x)的最大值;
(3)若f(x1)=f(x2)=0(x1<x2),求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).
(I)将S表示为 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施不能建设开发,且要求用栏栅隔开(栏栅要求在直线上),公共设施边界为曲线 的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设
的一部分,栏栅与矩形区域的边界交于点M、N,切曲线于点P,设 .
.
(I)将 (O为坐标原点)的面积S表示成f的函数S(t);
(O为坐标原点)的面积S表示成f的函数S(t);
(II)若 ,S(t)取得最小值,求此时a的值及S(t)的最小值.
,S(t)取得最小值,求此时a的值及S(t)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com