
某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: ),
), (单位:弧度).
(单位:弧度).
(I)将S表示为 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数 ,
, ,其中
,其中 且
且 .
.
(Ⅰ) 当 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若 时,函数
时,函数 有极值,求函数
有极值,求函数 图象的对称中心的坐标;
图象的对称中心的坐标;
(Ⅲ)设函数 (
( 是自然对数的底数),是否存在a使
是自然对数的底数),是否存在a使 在
在 上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
上为减函数,若存在,求实数a的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数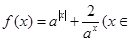 R,
R,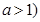 ,
,
(1)求函数f(x)的值域;
(2)记函数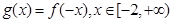 ,若
,若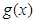 的最小值与
的最小值与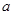 无关,求
无关,求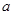 的取值范围;
的取值范围;
(3)若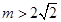 ,直接写出(不需给出演算步骤)关于
,直接写出(不需给出演算步骤)关于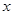 的方程
的方程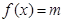 的解集
的解集
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com