
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 面
面![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() 面
面![]()
(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)求直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

【答案】(1)见解析(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)连接AC交BD于E,连接ME,可得PA∥面MBD,且ME是平面PAC与平面MDB的交线,得PA∥ME,即M是PC的中点;
(2)取AD中点,由(1)知OA、OE、OP两两垂直,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,求出![]() 所成角的余弦值,得到正弦值,进一步得到直线PA与MB所成角的正切值;
所成角的余弦值,得到正弦值,进一步得到直线PA与MB所成角的正切值;
(3)设在PA上是否存在点F,使二面角F﹣BD﹣M为直角,且![]() ,则由
,则由![]() ,得F(1﹣λ,0,
,得F(1﹣λ,0, ![]() ),分别求出平面MBD与平面FBD的一个法向量,由两法向量垂直求得λ值,可得存在点F,使二面角F﹣BD﹣M为直角,此时
),分别求出平面MBD与平面FBD的一个法向量,由两法向量垂直求得λ值,可得存在点F,使二面角F﹣BD﹣M为直角,此时![]() .
.
试题解析:
(1)证明:连![]() 交
交![]() 于
于![]() ,连
,连![]() .∵
.∵![]() 是矩形,∴
是矩形,∴![]() 是
是![]() 中点.又
中点.又![]() 面
面![]() ,且
,且![]() 是面
是面![]() 与面
与面![]() 的交线,∴
的交线,∴![]() ,∴
,∴![]() 是
是![]() 的中点.
的中点.
(2)取![]() 中点
中点![]() ,由(1)
,由(1)![]() ,
, ![]() ,
, ![]() 两两垂直.以
两两垂直.以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
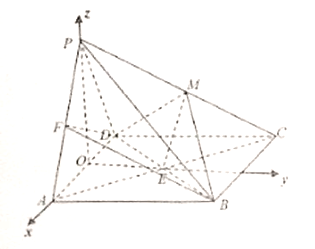
轴, ![]() 轴建立空间直角坐标系(如图),则各点坐标为
轴建立空间直角坐标系(如图),则各点坐标为
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 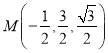 .
.
![]()
(3)设存在![]() 满足要求,且
满足要求,且![]() ,则由
,则由![]() 得
得![]() ,
,
平面![]() 的一个法向量为
的一个法向量为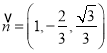 ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
, ![]() ,得
,得![]() ,解得
,解得![]() ,故存在
,故存在![]() ,使二面角
,使二面角![]() 为直角,此时
为直角,此时![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,![]() ,PA=AC=1.
,PA=AC=1.
(1)求证:AE⊥PB;
(2)求三棱锥C-ABE的体积.
(3)求二面角A-PB-C的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个“S点”.
的一个“S点”.
(1)证明:函数![]() 与
与![]() 不存在“S点”;
不存在“S点”;
(2)若函数![]() 与
与![]() 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;
(3)已知函数![]() ,
,![]() .对任意
.对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在“S点”,并说明理由.
内存在“S点”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的个数有( )
甲、乙两学生参与某考试,设命题![]() :甲考试及格,
:甲考试及格, ![]() :乙考试及格,则命题“至少有一位学生不及格”可表示为
:乙考试及格,则命题“至少有一位学生不及格”可表示为![]() .命题“对
.命题“对![]() ,都有
,都有![]() ”的否定为“
”的否定为“![]() ,使得
,使得![]() ”.“若
”.“若![]() ,则
,则![]() ”是假命题.④“
”是假命题.④“![]() ”是“
”是“![]() ”的必要不充分条件.⑤函数
”的必要不充分条件.⑤函数![]() 是偶函数
是偶函数
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)求续驶里程在![]() 的车辆数;
的车辆数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,下列四个命题中正确的是( )
,下列四个命题中正确的是( )
A.若![]() ,则
,则![]() 一定是锐角三角形
一定是锐角三角形
B.若![]() ,则
,则![]() 一定是等边三角形
一定是等边三角形
C.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
D.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
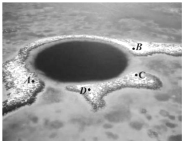
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com