
【题目】记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个“S点”.
的一个“S点”.
(1)证明:函数![]() 与
与![]() 不存在“S点”;
不存在“S点”;
(2)若函数![]() 与
与![]() 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;
(3)已知函数![]() ,
,![]() .对任意
.对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在“S点”,并说明理由.
内存在“S点”,并说明理由.
【答案】(1)证明见解析
(2)a的值为![]()
(3)对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
【解析】分析:(1)根据题中“S点”的定义列两个方程,根据方程组无解证得结论;(2)同(1)根据“S点”的定义列两个方程,解方程组可得a的值;(3)通过构造函数以及结合 “S点”的定义列两个方程,再判断方程组是否有解即可证得结论.
详解:解:(1)函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)= g′(x),得
![]() ,此方程组无解,
,此方程组无解,
因此,f(x)与g(x)不存在“S”点.
(2)函数![]() ,
,![]() ,
,
则![]() .
.
设x0为f(x)与g(x)的“S”点,由f(x0)与g(x0)且f′(x0)与g′(x0),得
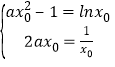 ,即
,即 ,(*)
,(*)
得![]() ,即
,即![]() ,则
,则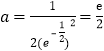 .
.
当![]() 时,
时,![]() 满足方程组(*),即
满足方程组(*),即![]() 为f(x)与g(x)的“S”点.
为f(x)与g(x)的“S”点.
因此,a的值为![]() .
.
(3)对任意a>0,设![]() .
.
因为![]() ,且h(x)的图象是不间断的,
,且h(x)的图象是不间断的,
所以存在![]() ∈(0,1),使得
∈(0,1),使得![]() ,令
,令![]() ,则b>0.
,则b>0.
函数![]() ,
,
则![]() .
.
由f(x)与g(x)且f′(x)与g′(x),得
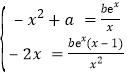 ,即
,即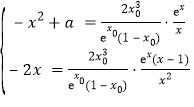 (**)
(**)
此时,![]() 满足方程组(**),即
满足方程组(**),即![]() 是函数f(x)与g(x)在区间(0,1)内的一个“S点”.
是函数f(x)与g(x)在区间(0,1)内的一个“S点”.
因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.


科目:高中数学 来源: 题型:
【题目】已知动圆![]() 恒过点
恒过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求圆心![]() 的轨迹方程;
的轨迹方程;
(2)若过点![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() ,
, ![]() 两点,直线
两点,直线![]() ,
, ![]() (
(![]() 为坐标原点)分别交直线
为坐标原点)分别交直线![]() 于点
于点![]() ,
, ![]() ,证明:以
,证明:以![]() 为直径的圆被
为直径的圆被![]() 轴截得的弦长为定值.
轴截得的弦长为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司研发芯片耗费资金2千万元,现在准备投入资金进行生产.经市场调查与预测,生产A芯片的毛收入![]() (平万元)与投入的资金x(千万元)成正比,已知每投入1千万元,获得毛收入0.25千万元;生产B芯片的毛收入
(平万元)与投入的资金x(千万元)成正比,已知每投入1千万元,获得毛收入0.25千万元;生产B芯片的毛收入![]() (千万元)与投入的资金x(千万元)的函数关系式为
(千万元)与投入的资金x(千万元)的函数关系式为![]() ,其图像如图所示.
,其图像如图所示.

(1)试分别求出生产A,B两种芯片的毛收入与投入资金的函数关系式.
(2)如果公司只生产一种芯片,生产哪种芯片毛收入更大?
(3)现在公司准备投入4亿元资金同时生产A,B两种芯片,设投入x千万元生产B芯片,用![]() 表示公司所获利润,当x为多少时,可以获得最大利润?并求最大利润.(利润=A芯片毛收入+B芯片毛收入-研发耗费资金)
表示公司所获利润,当x为多少时,可以获得最大利润?并求最大利润.(利润=A芯片毛收入+B芯片毛收入-研发耗费资金)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,每年高考结束后,处于休养状态的高中毕业生旅游动机强烈,旅游可支配收入日益增多,可见高中毕业生旅游是一个巨大的市场.为了解高中毕业生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某市的1000名毕业生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)求所得样本的中位数(精确到百元);
(2)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
(3)已知本数据中旅游费用支出在![]() 范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为
范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 面
面![]() ,且
,且![]() 是边长为2的等边三角形,
是边长为2的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() 面
面![]()
(1)求证: ![]() 是
是![]() 的中点;
的中点;
(2)求直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)在![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 为直角?若存在,求出
为直角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂现有职工320人,平均每人每年可创利20万元.该工厂打算购进一批智能机器人(每购进一台机器人,将有一名职工下岗).据测算,如果购进智能机器人不超过100台,每购进一台机器人,所有留岗职工(机器人视为机器,不作为职工看待)在机器人的帮助下,每人每年多创利2千元,每台机器人购置费及日常维护费用折合后平均每年2万元,工厂为体现对职工的关心,给予下岗职工每人每年4万元补贴;如果购进智能机器人数量超过100台,则工厂的年利润![]() 万元(x为机器人台数且x<320).
万元(x为机器人台数且x<320).
(1)写出工厂的年利润y与购进智能机器人台数x的函数关系.
(2)为获得最大经济效益,工厂应购进多少台智能机器人?此时工厂的最大年利润是多少?(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com