
【题目】一个多面体的直观图及三视图如图所示,![]() 分别是
分别是![]() 的中点.
的中点.
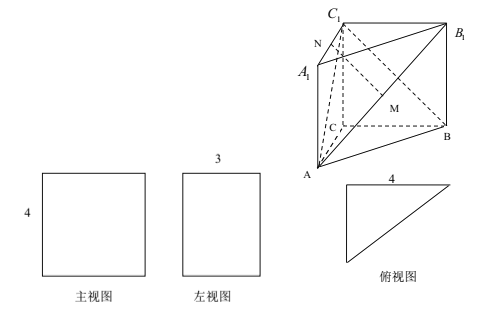
(I)求证:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.
【答案】(I)证明见解析;(II)![]() .
.
【解析】
试题分析:(I)由直观图及三视图可知,该几何体为直三棱柱,底面为直角三角形,因此![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,写出各点坐标,证明
轴,建立空间直角坐标系,写出各点坐标,证明![]() 即可;(II)求平面
即可;(II)求平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,然后计算出
,然后计算出![]() 的值,通过观察图形确定二面角
的值,通过观察图形确定二面角![]() 的余弦值与
的余弦值与![]() 关系即可.
关系即可.
试题解析:(I)证明:由三视图可知,在这个多面体的直观图中,![]() ,且
,且![]() ……………………………1分
……………………………1分
因此![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系, ……………………………2分
轴,建立空间直角坐标系, ……………………………2分
则由已知可得:![]() ,
,
故![]() ,
,
![]() ……………………………3分
……………………………3分
即![]() 4分
4分
即![]() ,
,
而![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .……………………………6分
.……………………………6分
(II)解:设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
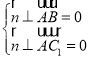 ,
,![]() ,
,![]() ,
,
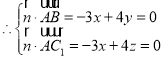 ,
,
令![]() ,可得
,可得![]() ,
,
![]() ,……………………………2分
,……………………………2分
由已知可得![]() 平面
平面![]() ,
,
![]() 是平面
是平面![]() 的一个法向量,…………………………10分
的一个法向量,…………………………10分
设二面角![]() 的平面角为
的平面角为![]() ,则有:
,则有: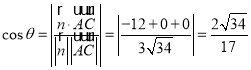 ,
,
![]() 所求二面角的余弦值是
所求二面角的余弦值是![]() .…………………………12分
.…………………………12分


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:![]() ,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
,且每处理一顿二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家每月至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两枚均匀的硬币和一枚不均匀的硬币,其中不均匀的硬币抛掷后出现正面的概率为![]() ,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
,小华先抛掷这三枚硬币,然后小红再抛掷这三枚硬币.
(1)求小华抛得一个正面两个反面且小红抛得两个正面一个反面的概率;
(2)若用![]() 表示小华抛得正面的个数,求
表示小华抛得正面的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数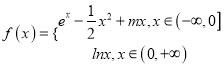 ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 时,函数
时,函数![]() 在
在![]() 内是增函数,求
内是增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数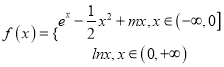 ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 时,函数
时,函数![]() 在
在![]() 内是增函数,求
内是增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
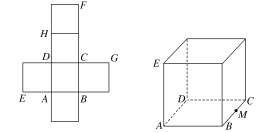
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如下.通过计算,可以得到对应的回归方程![]() =-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )
=-2.352x+147.767,根据以上信息,判断下列结论中正确的是( )
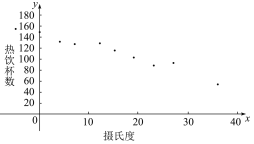
摄氏温度 | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
热饮杯数 | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
A.气温与热饮的销售杯数之间成正相关
B.当天气温为2℃时,这天大约可以卖出143杯热饮
C.当天气温为10℃时,这天恰卖出124杯热饮
D.由于x=0时,![]() 的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性
的值与调查数据不符,故气温与卖出热饮杯数不存在线性相关性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com