
【题目】已知函数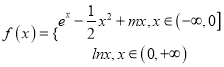 ,
, ![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 时,函数
时,函数![]() 在
在![]() 内是增函数,求
内是增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() 、
、![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)不存在.
;(3)不存在.
【解析】试题分析:
(1)利用导函数与切线的关系得到方程,解方程可得![]() ,
, ![]() ;
;
(2)函数为增函数,则![]() 即
即![]() 在
在![]() 内恒成立,处理恒成立问题可得
内恒成立,处理恒成立问题可得![]() 的取值范围是
的取值范围是![]() ;
;
(3) 假设![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线平行,则
处的切线平行,则![]() ,
, ![]() ①,讨论可得矛盾,假设不成立,
①,讨论可得矛盾,假设不成立,
故![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.
试题解析:(1)当![]() 时,
时, ![]() ,导数
,导数![]() ,
,
![]() ,
,
即函数![]() 的图象在
的图象在![]() 处的切线斜率为
处的切线斜率为![]() ,切点为
,切点为![]() ,
,
![]() 函数
函数![]() 的图象在
的图象在![]() 处的切线方程为
处的切线方程为![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
;
(2)![]() 时,函数
时,函数![]() 在
在![]() 的解析式是
的解析式是![]() ,
,
导数![]() ,
,
![]() 函数
函数![]() 在
在![]() 内是增函数,
内是增函数,
![]() 即
即![]() 在
在![]() 内恒成立,
内恒成立, ![]() ,
,
![]() 时,
时, ![]() .
.
![]() ,故
,故![]() 的取值范围是
的取值范围是![]() ;
;
(3)假设![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线平行,
处的切线平行,
设点![]() ,
, ![]() ,
, ![]() ,
,
则由题意得点![]() 、
、![]() 的横坐标与中点
的横坐标与中点![]() 的横坐标相等,且为
的横坐标相等,且为![]() ,
,
![]() 时,
时, ![]() ,
, ![]() ,
,
![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
由于两切线平行,则![]() ,
,
即![]() ,则两边同乘以
,则两边同乘以![]() ,得,
,得,
![]() ,
,
![]()
![]() ,
, 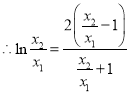 ,
,
设![]() ,则
,则![]() ,
, ![]() ①,
①,
令![]() ,
, ![]() ,则
,则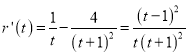 ,
,
![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
, ![]() ,这与①矛盾,假设不成立,
,这与①矛盾,假设不成立,
故![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线不平行.
处的切线不平行.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾, 5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元,距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
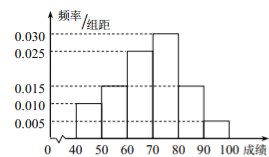
, ![]() 五组,并作出如下频率分布直方图(图1):
五组,并作出如下频率分布直方图(图1):

(1)试根据频率分布直方图估计小区平均每户居民的平均损失;
(同一组中的数据用该组区间的中点值作代表);
(2)小明向班级同学发出倡议,为该小区居民捐款,现从损失超过6000元的居民中随机
抽出2户进行捐款援助,求抽出的2户居民损失均超过8000元的概率;
(3)台风后区委会号召该小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如下表,
在图2表格空白外填写正确数字,并说明是否有95%以上的把握认为捐款数额超过或
不超过500元和自身经济损失是否超过4000元有关?
经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
捐款超过500元 | 30 | ||
捐款不超过500元 | 6 | ||
合计 |
附:临界值参考公式:  ,
, ![]() .
.
| 0.15 | 0.10 | 0.05 /td> | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
(2)将上述调査所得的频率视为概率,现从参赛学生中,任意抽取![]() 名学生,记“获奖”学生人数为
名学生,记“获奖”学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
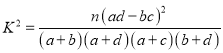 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 分别交
分别交![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(3)在第(2)问的条件下,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设cn=an+bn,求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
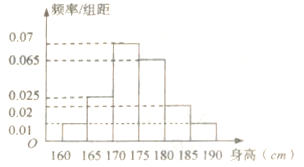
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com