
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
分析 利用公式求出$\hat{a}$,即可得回归直线方程$\stackrel{∧}{y}$=10.5x+$\stackrel{∧}{a}$,当x=20时,求解y即可.
解答 解:样本平均数$\overline{x}$=5,$\overline{y}$=54,回归直线方程为$\stackrel{∧}{y}$=10.5x+$\stackrel{∧}{a}$,
∴$\hat{b}$=10.5,
∴$\hat{a}$=54-10.5×5=1.5
则回归直线方程为$\stackrel{∧}{y}$=10.5x+1.5,
当x=20时,y=10.5×20+1.5=211.5.
故答案为:211.5.
点评 本题考查线性回归方程的求法,考查最小二乘法,属于基础题.


科目:高中数学 来源: 题型:填空题
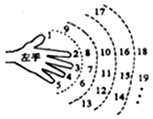 某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.
某小朋友按如下规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,7中指,8食指,9大拇指,10食指,…,一直数到2017时,对应的指头是大拇指.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com