
分析 求出函数的导数,分别求出f($\frac{π}{6}$),f′($\frac{π}{6}$)的值,求出切线方程即可.
解答 解:f(x)=sin2(3x-$\frac{π}{6}$)=$\frac{1-cos(6x-\frac{π}{3})}{2}$,f($\frac{π}{6}$)=$\frac{3}{4}$,
f′(x)=3sin(6x-$\frac{π}{3}$),则f′($\frac{π}{6}$)=$\frac{3\sqrt{3}}{2}$,
故在x=$\frac{π}{6}$处的切线方程为y-$\frac{3}{4}$=$\frac{3\sqrt{3}}{2}$(x-$\frac{π}{6}$),
整理得:$\frac{3\sqrt{3}}{2}$x-y-$\frac{\sqrt{3}}{4}$π+$\frac{3}{4}$=0.
点评 本题考查了切线方程问题,考查导数的应用,是一道基础题.


科目:高中数学 来源: 题型:填空题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 70 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
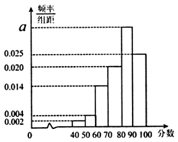 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com