
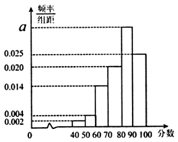
 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
分析 (I)由频率和为1列方程求出a的值,根据比例关系求出不满意的人数;
(II)按分层抽样原理抽取6人,利用列举法求出所有的基本事件数,计算对应的概率值;
(III)计算师生的满意指数,即可得出结论.
解答 解:(I)由频率和为1,得
(0.002+0.004+0.014+0.020+a+0.025)×10=1,
解得a=0.035,
设不满意的人数为x,则
(0.002+0.004):(0.014+0.020)=x:136,
解得x=24;
(II)按评分分层抽取6人,应在评分在[40,50)的师生中抽取2人,分别记作A、B,
在评分在[50,60)的师生中抽取4人,分别记为c、d、e、f,
从这6人中选2人的所有基本事件为
AB、Ac、Ad、Ae、Af、Bc、Bd、Be、Bf、cd、ce、cf、de、df、ef共15种,
其中恰有1人评分在[40,50)包含的基本事件为
Ac、Ad、Ae、Af、Bc、Bd、Be、Bf共8种,
记“2人中恰有1人的评分在[40,50)”为事件A,则P(A)=$\frac{8}{15}$;
(III)师生的满意指数为
$\frac{1}{100}$×(45×0.02+55×0.04+65×0.14+75×0.2+85×0.35+95×0.25)=0.807;
师生的满意指数不低于0.8,可获评“教学管理先进单位”.
点评 本题考查了频率分布直方图与列举法求古典概型的概率问题,是中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当a>1时,函数y=ax是增函数,因为2>1,所以函数y=2x是增函数,这种推理是合情推理 | |
| B. | 在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c,则a∥c,将此结论放到空间中也是如此.这种推理是演绎推理 | |
| C. | 命题$P:?{x_0}∈R,{e^{x_0}}<{x_0}$的否定是¬P:?x∈R,ex>x | |
| D. | 若分类变量X与Y的随机变量K2的观测值k越小,则两个分类变量有关系的把握性越小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.
如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x2-8x+11 | B. | f(x)=-2x2+8x-1 | C. | f(x)=2x2-4x+3 | D. | f(x)=-2x2+4x+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 种子粒数n | 25 | 70 | 130 | 700 | 2 015 | 3 000 | 4 000 |
| 发芽粒数m | 24 | 60 | 116 | 639 | 1 819 | 2 713 | 3 612 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com