
分析 (Ⅰ)求出导数,讨论导数的符号,确定其单调区间,从而确定极值.
(Ⅱ)g(x)定义域是(0,+∞),$g'(x)=x+\frac{1}{x}-2a$.分以下两种情况讨论,①若a≤1,②若a>1.
解答 解:(Ⅰ)f(x)定义域是(0,+∞),$f'(x)=\frac{{1-3{x^2}}}{x}$,令f'(x)=0得$x=\frac{{\sqrt{3}}}{3}$.
列表
| x | $(0,\frac{{\sqrt{3}}}{3})$ | $\frac{{\sqrt{3}}}{3}$ | (0,+∞) |
| f'(x) | + | 0 | - |
| f(x) | ↗ | $-\frac{1}{2}-\frac{1}{2}ln3$ | ↘ |
点评 本题考查了导数的综合应用,利用导数求极值、最值,考查了计算能力,属于压轴题,


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | g(x)为奇函数 | B. | g(x)为偶函数 | ||
| C. | g(x)在$[0,\frac{π}{3}]$上单调递增 | D. | g(x)的一个对称中心为$(-\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
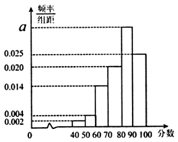 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com