
 如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.
如图,菱ABCD与四边形BDEF相交于BD,∠ABC=120°,BF⊥平面ABCD,DE∥BF,BF=2DE,AF⊥FC,M为CF的中点,AC∩BD=G.分析 (I)取BC的中点N,连接GN,GM,MN.由MN∥BF∥DE,GN∥CD可得平面GMN∥平面CDE,故而GM∥平面CDE;
(II)以G为原点,建立空间坐标系,求出平面ACE的法向量$\overrightarrow{m}$和$\overrightarrow{AM}$的坐标,计算$\overrightarrow{m}$和$\overrightarrow{AM}$的夹角即可得出结论.
解答 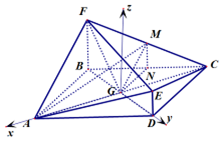 证明:(Ⅰ)取BC的中点N,连接GN,GM,MN.
证明:(Ⅰ)取BC的中点N,连接GN,GM,MN.
因为G为菱形对角线的交点,所以G为AC中点,
又N为BC中点,所以GN∥CD,
又因为M,N分别为FC,BC的中点,
所以MN∥FB,又因为DE∥BF,
所以DE∥MN,
又MN∩GN=N,
所以平面GMN∥平面CDE,
又GM?平面GMN,
所以GM∥平面CDE.
(Ⅱ)连接GF,设菱形的边长AB=2,则由∠ABC=120°,得$GB=GD=1,GA=GC=\sqrt{3}$,
又因为AF⊥FC,所以$FG=GA=\sqrt{3}$,
则在直角三角形GBF中,$BF=\sqrt{2}$,所以$DE=\frac{{\sqrt{2}}}{2}$,
以G为坐标原点,分别以GA,GD所在直线为x轴,y轴,建立空间直角坐标系G-xyz,
则$G(0,0,0),A(\sqrt{3},0,0),E(0,1,\frac{{\sqrt{2}}}{2}),F(0,-1,\sqrt{2})$,$M(-\frac{{\sqrt{3}}}{2},-\frac{1}{2},\frac{{\sqrt{2}}}{2})$
则$\overrightarrow{GA}=(\sqrt{3},0,0),\overrightarrow{GE}=(0,1,\frac{{\sqrt{2}}}{2})$,
设$\overrightarrow m=(x,y,z)$为平面ACE的一个法向量,则$\left\{{\begin{array}{l}{\overrightarrow m•\overrightarrow{GA}=0}\\{\overrightarrow m•\overrightarrow{GE}=0}\end{array}}\right.$即$\left\{{\begin{array}{l}{\sqrt{3}x=0}\\{y+\frac{{\sqrt{2}}}{2}z=0}\end{array}}\right.$,
令$z=\sqrt{2}$,得$\overrightarrow m=(0,-1,\sqrt{2})$,
又$\overrightarrow{AM}=(-\frac{{3\sqrt{3}}}{2},-\frac{1}{2},\frac{{\sqrt{2}}}{2})$,所以$cos?\overrightarrow{AM},\overrightarrow m)=\frac{{\overrightarrow{AM}•\overrightarrow m}}{{|\overrightarrow{AM}||\overrightarrow m|}}=\frac{{\frac{1}{2}+1}}{{\sqrt{1+2}\sqrt{\frac{27}{4}+\frac{1}{4}+\frac{1}{2}}}}=\frac{{\sqrt{10}}}{10}$=$\frac{\overrightarrow{AM}•\overrightarrow{m}}{|\overrightarrow{AM}||\overrightarrow{m}|}$=$\frac{\frac{3}{2}}{\sqrt{3}•\frac{\sqrt{30}}{2}}$=$\frac{\sqrt{10}}{10}$,
所以直线AM与平面ACE所成角的正弦值为$\frac{\sqrt{10}}{10}$.
点评 本题考查了线面平行的判定,空间向量与线面角的计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | g(x)为奇函数 | B. | g(x)为偶函数 | ||
| C. | g(x)在$[0,\frac{π}{3}]$上单调递增 | D. | g(x)的一个对称中心为$(-\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
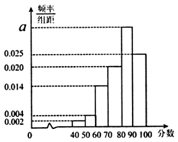 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com