
分析 根据直线和圆相切求出a,b的关系式,结合基本不等式进行求解即可.
解答 解:圆C:(x-a)2+(y-b)2=10的圆心(a,b)半径为:$\sqrt{10}$,
∵直线和圆相切,
∴$\frac{|a+2b|}{\sqrt{5}}=\sqrt{10}$,
∵圆心C在直线l的上方,
∴a+2b>0,从而a+2b=5$\sqrt{2}$,
∴ab=$\frac{1}{2}$a(2b)≤$\frac{1}{2}×(\frac{a+2b}{2})^{2}$=$\frac{25}{4}$,当且仅当a=2b,即a=$\frac{5\sqrt{2}}{2}$,b=$\frac{5\sqrt{2}}{4}$时取等号,
故ab的最大值为$\frac{25}{4}$,
故答案为:$\frac{25}{4}$.
点评 本题主要考查直线和圆相切的应用以及基本不等式的应用,根据相切关系建立a,b的关系是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | g(x)为奇函数 | B. | g(x)为偶函数 | ||
| C. | g(x)在$[0,\frac{π}{3}]$上单调递增 | D. | g(x)的一个对称中心为$(-\frac{π}{2},0)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
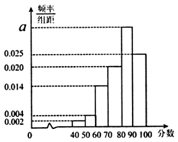 某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
某地教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的学生中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:| 满意度评分 | 低于60分 | 60分到79分 | 80分到89分 | 90分及以上 |
| 满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com