解:(1)∵平面ABFE⊥平面ABCD,平面ABFE∩平面ABCD=AB,CB⊥AB,
∴CB⊥平面ABFE,结合AF⊆平面ABFE,
∴AF⊥CB
在直角梯形ABFE中,AB∥EF,∠EAB=90°AE=EF=2
∴AF=
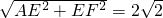
?∠FAB=45°
△ABF中,AB=4,根据余弦定理得:
BF=
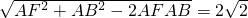
∴BF
2+AF
2=AB
2?AF⊥FB.
∵CB∩FB=B,
∴AF⊥平面BCF.
(2)分别取CD、AB中点G、H,连接GH、GF和FH
由(1)的证明知三棱柱DAE-GHF是直三棱柱三棱柱DAE-GHF
∴V
三棱柱DAE-GHF=S
△AED•EF=

AD•AE•EF=4
又∵平面ABFE⊥平面ABCD,平面ABFE∩平面ABCD=AB,
等腰Rt△AFB中,中线FH⊥AB,
∴FH⊥平面ABCD,FH是四棱锥F-BCGH的高线
∴V
四棱锥F-BCGH=

S
矩形BCGH•FH=

•GC•GH•FH=

所以多面体ABCDEF的体积V=V
三棱柱DAE-GHF+V
四棱锥F-BCGH=

分析:(1)首先利用平面ABFE与平面ABCD互相垂直,结合面面垂直的性质得到AF与CB垂直,然后利用余弦定理在△ABF中计算出BF的长,从而BF
2+AF
2=AB
2,得出AF⊥FB,最后运用直线与平面垂直的判定定理,得到AF⊥平面BCF;
(2)分别取CD、AB中点G、H,连接GH、GF和FH,将多面体分割为一个直三棱柱和一个四棱锥.然后利用(1)中的线面垂直、线线垂直关系和线段长度,分别计算出直三棱柱和四棱锥的体积,最后可求出求多面体ABCDEF的体积.
点评:本题是一道立体几何的综合题,着重考查了利用棱柱、棱锥、棱台的体积公式求组合几何体的面积、体积问题和平面与平面垂直的性质及直线与平面垂直的判定等知识点,属于中档题.

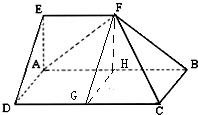
 如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
如图,在多面体ABCDEF中,四边形ABCD是矩形,在四边形ABFE中,AB∥EF,∠EAB=90°,AB=4,AD=AE=EF=2,平面ABFE⊥平面ABCD.
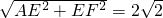 ?∠FAB=45°
?∠FAB=45°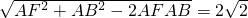
 AD•AE•EF=4
AD•AE•EF=4 S矩形BCGH•FH=
S矩形BCGH•FH= •GC•GH•FH=
•GC•GH•FH=



 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=