
在数列{an}和等比数列{bn}中,a1=0,a3=2,bn=2an+1(n∈N*).
(1)求数列{bn}及{an}的通项公式;
(2)若cn=an·bn,求数列{cn}的前n项和Sn.
(1)an=n-1(2)Sn=4+(n-2)·2n+1
【解析】(1)方法一,依题意b1=2,b3=23=8,
设数列{bn}的公比为q,由bn=2an+1>0,可知q>0.
由b3=b1·q2=2·q2=8,得q2=4,又q>0,则q=2,
故bn=b1qn-1=2·2n-1=2n,
又由2an+1=2n,得an=n-1.
(2)依题意cn=(n-1)·2n.
Sn=0·21+1·22+2·23+…+(n-2)·2n-1+(n-1)·2n ,①
则2Sn=0·22+1·23+2·24+…+(n-2)·2n+(n-1)·2n+1,②
①-②得
-Sn=22+23+…+2n-(n-1)·2n+1=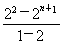 -(n-1)·2n+1,
-(n-1)·2n+1,
即-Sn=-4+(2-n)·2n+1,故Sn=4+(n-2)·2n+1.
方法二,(1)依题意{bn}为等比数列,则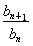 =q(常数),
=q(常数),
由bn=2an+1>0,可知q>0.
由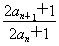 =2an+1-an=q,
=2an+1-an=q,
得an+1-an=log2q(常数),故{an}为等差数列.
设{an}的公差为d,由a1=0,a3=a1+2d=0+2d=2,得d=1,
故an=n-1.
(2)同方法一.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题五练习卷(解析版) 题型:选择题
已知m,n是空间两条不同的直线,α,β,γ是三个不同的平面,则下列命题中为真的是( )
A.若α∥β,m?α,n?β,则m∥n
B.若α∩γ=m,β∩γ=n,m∥n,则α∥β
C.若m?β,α⊥β,则m⊥α
D.若m⊥β,m∥α,则α⊥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题七练习卷(解析版) 题型:填空题
抽样统计甲、乙两位射击运动员的5次训练成绩(单位:环),结果如下:
运动员 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
甲 | 87 | 91 | 90 | 89 | 93 |
乙 | 89 | 90 | 91 | 88 | 92 |
则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题一练习卷(解析版) 题型:选择题
设a=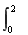 (1-3x2)dx+4,则二项式x2+
(1-3x2)dx+4,则二项式x2+ 6的展开式中不含x3项的系数和是( )
6的展开式中不含x3项的系数和是( )
A.-160 B.160 C.161 D.-160
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集9讲练习卷(解析版) 题型:选择题
已知数列{an}是公差为2的等差数列,且a1,a2,a5成等比数列,则数列{an}的前5项和S5=( )
A.20 B.30 C.25 D.40
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集9讲练习卷(解析版) 题型:选择题
一个由正数组成的等比数列,它的前4项和是前2项和的5倍,则此数列的公比为( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集7讲练习卷(解析版) 题型:解答题
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的部分图像如图所示,

(1)求ω,φ的值;
(2)设g(x)=2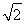 f
f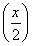 f
f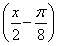 -1,当x∈[0,
-1,当x∈[0,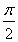 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学文复习二轮作业手册新课标·通用版限时集5讲练习卷(解析版) 题型:选择题
“m<0”是“函数f(x)=m+log2x(x≥1)存在零点”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com