
���� ��1����ȥ�����������ɵõ�����C����ͨ���̣����ü�������ֱ�����껥�����ֱ��l��ֱ�����귽�̣�
��2�����Բ��Բ����뾶���������������꣬Ȼ����⼫���꣮
���  �⣺��1������$C��\left\{\begin{array}{l}x=\sqrt{3}cos��+sin��\\ y=\sqrt{3}sin��-cos��\end{array}\right.$��
�⣺��1������$C��\left\{\begin{array}{l}x=\sqrt{3}cos��+sin��\\ y=\sqrt{3}sin��-cos��\end{array}\right.$��
�ɵã�$\left\{\begin{array}{l}{{x}^{2}=3co{s}^{2}��+2\sqrt{3}sin��cos��+si{n}^{2}��}\\{{y}^{2}=3si{n}^{2}��-2\sqrt{3}sin��cos��+co{s}^{2}��}\end{array}\right.$��
����C����ͨ���̣�x2+y2=4��
ֱ��$l����sin��{��+\frac{��}{6}}��=1$=$\frac{\sqrt{3}}{2}��sin��+\frac{1}{2}��cos��$��
ֱ��l��ֱ�����귽�̣�x+$\sqrt{3}$y-2=0��
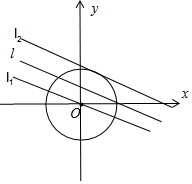
��2����ԲC��Բ�ģ�0��0���뾶Ϊ��2��
��Բ��C��ֱ�ߵľ���Ϊ1��
������������ƽ��ֱ��l1�� l2�ϣ���ͼ��
ֱ��l1�� l2��l�ľ���Ϊ1��
l1��x+$\sqrt{3}y$=0��l2��x+$\sqrt{3}y$-4=0��
$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{x+\sqrt{3}y=0}\end{array}\right.$���ɵ�$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=-1}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=1}\end{array}\right.$��
�������㣨-$\sqrt{3}$��1������$\sqrt{3}$��-1����
$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{x+\sqrt{3}y-4=0}\end{array}\right.$����ã�1��$\sqrt{3}$����
��������ļ�����ֱ�Ϊ����2��$\frac{11��}{6}$������2��$\frac{5��}{6}$������2��$\frac{��}{3}$��
���� ���⿼��ֱ�ߵļ����귽�̣�Բ�IJ�����������ͨ���̵Ļ�����ֱ����Բ��λ�ù�ϵ��Ӧ�ã��������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{4}{3}$ | B�� | -$\frac{3}{4}$ | C�� | -$\frac{4}{5}$ | D�� | ��$\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
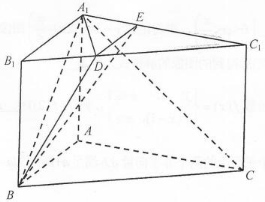 ��ͼ����ֱ������ABC-A1B1C1�У���֪��BAC=90�㣬AB=a��AC=2��AA1=1����D����B1C1�ϣ���B1D��DC1=1��3������D��DE��A1B1��A1C1�ڵ�E��
��ͼ����ֱ������ABC-A1B1C1�У���֪��BAC=90�㣬AB=a��AC=2��AA1=1����D����B1C1�ϣ���B1D��DC1=1��3������D��DE��A1B1��A1C1�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ | B�� | ��Ҫ����� | ||
| C�� | ��Ҫ | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1B1C1�У���ACB=90�㣬E��F��G�ֱ���AA1��AC��BB1���е㣬��CG��C1G��
��ͼ����ֱ������ABC-A1B1C1�У���ACB=90�㣬E��F��G�ֱ���AA1��AC��BB1���е㣬��CG��C1G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com