练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．如图AB是半圆O的直径，C，D是弧AB的三等分点，M，N是线段AB的三等分点，若OA=6，则$\overrightarrow{MC}•\overrightarrow{ND}$=26

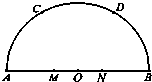
    分析 建立坐标系，求出各点坐标得出$\overrightarrow{MC}，\overrightarrow{ND}$的坐标进行计算．

    解答 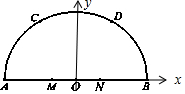解：以AB为x轴，以O为原点建立平面直角坐标系，如图所示：
    则M（-2，0），N（2，0），C（-3，3$\sqrt{3}$），D（3，3$\sqrt{3}$），
    ∴$\overrightarrow{MC}$=（-1，3$\sqrt{3}$），$\overrightarrow{ND}$=（1，3$\sqrt{3}$），
    ∴$\overrightarrow{MC}•\overrightarrow{ND}$=-1+27=26．
    故答案为26．

    点评 本题考查了平面向量的数量积运算，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．已知在平面直角坐标系xoy中，O为坐标原点，曲线$C：\left\{\begin{array}{l}x=\sqrt{3}cosα+sinα\\ y=\sqrt{3}sinα-cosα\end{array}\right.$（α为参数），在以平面直角坐标系的原点为极点，x轴的正半轴为极轴，取相同单位长度的极坐标系，直线$l：ρsin（{θ+\frac{π}{6}}）=1$．
    （1）求曲线C的普通方程和直线l的直角坐标方程；
    （2）曲线C上恰好存在三个不同的点到直线l的距离相等，分别求出这三个点的极坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知定义在R上的奇函数f（x）满足f（4-x）=f（x），f（-1）=6，数列{an}的前n项和为Sn，且a1=-1，Sn=2an+n （n∈N﹡），则f（a5）+f（a6）=-12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若函数f（x）=x2+aln（x+1）在（-1，+∞）上是增函数，则a的取值范围是（　　）
    A．[0，+∞）B．（0，+∞）C．（$\frac{1}{2}$，+∞）D．[$\frac{1}{2}$，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．用数字1，2，3，4，5组成的没有重复数字的五位偶数的个数是（　　）
    A．120B．60C．50D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．为了检测某种产品的质量，抽取了一个容量为100的样本，数据分组如下：
    分组频数频率
    [10.75，10.85）3
    [10.85，10.95）9
    [10.95，11.05）13
    [11.05，11.15）16
    [11.15，11.25）26
    [11.25，11.35）20
    [11.35，11.45）7
    [11.45，11.55）a
    [11.55，11.65）m0.02
    （1）求出表中a，m的值；
    （2）画出频率分布直方图；
    （3）根据频率分布直方图估计这组数据的众数、中位数和平均数；
    （4）根据上述图表，估计数据落在[10.95，11.35）范围内的可能性有百分之几？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

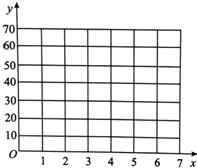    5．为了探究车流量与PM2.5的浓度是否相关，现采集到北方某城市2015年12月份星期一到星期日某一时间段车流量与PM2.5的数据如表：
    时间星期一星期二星期三星期四星期五星期六星期日
    车流量x（万辆）1234567
    PM2.5的浓度y
    （微克/立方米）    		27313541495662
    （1）在表中画出车流量与PM2.5浓度的散点图．
    （2）求y关于x的线性回归方程；
    （3）①利用所求回归方程，预测该市车流量为8万辆时，PM2.5的浓度；
    ②规定当一天内PM2.5的浓度平均值在（0，50]内，空气质量等级为优；当一天内PM2.5的浓度平均值在（50，100]内，空气质量等级为良，为使该市某日空气质量等级为优或良，则应控制当天车流量在多少万辆以内（结果以万辆为单位，保留整数）
    参考公式：回归直线的方程是$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知f（x）=|1-$\frac{1}{x}$|，若存在实数a，b（a＜b），使得y=f（x）在[a，b]上的值域为[ma，mb]，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若点（x，y）在曲线y=|x|与y=2所围成的封闭区域内（包括边界），则2x-y的最大值为（　　）
    A．-6B．6C．2D．0

    查看答案和解析>>

    同步练习册答案