
| A. | [0,+∞) | B. | (0,+∞) | C. | ($\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,+∞) |
分析 求出函数的导数,问题转化为a≥-2x2-2x在(-1,+∞)恒成立,令g(x)=-2x2-2x,(x>-1),根据函数的单调性求出a的范围即可.
解答 解:f′(x)=2x+$\frac{a}{x+1}$=$\frac{{2x}^{2}+2x+a}{x+1}$,
若函数f(x)=x2+aln(x+1)在(-1,+∞)上是增函数,
则2x2+2x+a≥0在(-1,+∞)恒成立,
即a≥-2x2-2x在(-1,+∞)恒成立,
令g(x)=-2x2-2x,(x>-1),
g(x)在(-1,-$\frac{1}{2}$)递增,在(-$\frac{1}{2}$,+∞)递减,
故g(x)的最大值是g(-$\frac{1}{2}$)=$\frac{1}{2}$,
故a≥$\frac{1}{2}$,
故选:D.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,是一道中档题.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
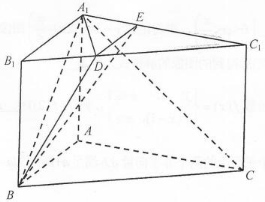 如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上,且B1D:DC1=1:3.过点D作DE∥A1B1交A1C1于点E.
如图,在直三棱柱ABC-A1B1C1中,已知∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上,且B1D:DC1=1:3.过点D作DE∥A1B1交A1C1于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,-1) | B. | ( 1,0) | C. | (1,-$\frac{π}{2}$) | D. | (1,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
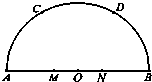
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
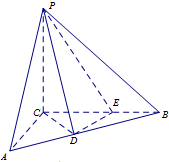 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2,AC=$\frac{3}{2}$.
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=3,∠ACB=$\frac{π}{2}$,D,E分别为线段AB,BC上的点,且CD=DE=$\sqrt{2}$,CE=2,AC=$\frac{3}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com