
分析 (1)先求出f(x)的定义域,令f′(x)>0解出增区间,令f′(x)<0解出减区间;
(2)令f′(x)=0在定义域上有两解,得出a的大致范围,把极值点代入解析式解不等式f(x1)+f(x2)>0即可.
解答 解:(1)a=$\frac{1}{2}$时,f(x)=ln(1+$\frac{1}{2}$x)-$\frac{2x}{x+2}$,f(x)的定义域为(-2,+∞).
f′(x)=$\frac{1}{x+2}$-$\frac{4}{(x+2)^{2}}$=$\frac{x-2}{(x+2)^{2}}$,
∴当-2<x<2时,f′(x)<0,当x>2时,f′(x)>0,
∴f(x)在(-2,2)上单调递减,在(2,+∞)上低调递增.
(2)f(x)的定义域为(-$\frac{1}{a}$,+∞),
f′(x)=$\frac{a}{1+ax}$-$\frac{4}{(x+2)^{2}}$=$\frac{a(x+2)^{2}-4(1+ax)}{(1+ax)(x+2)^{2}}$.
∵f(x)存在两个极值点x1,x2,
∴f′(x)=0在(-$\frac{1}{a}$,+∞)上有两解.
即ax2+4a-4=0在(-$\frac{1}{a}$,+∞)上有两解.∴4-4a>0.即0<a<1.
解ax2+4a-4=0得x=±$\sqrt{\frac{4-4a}{a}}$,
∴-$\sqrt{\frac{4-4a}{a}}$>-$\frac{1}{a}$,解得a$≠\frac{1}{2}$.
∵f(x1)+f(x2)>0,
∴ln(1+ax1)+ln(1+ax2)>$\frac{2{x}_{1}}{{x}_{1}+2}+\frac{2{x}_{2}}{{x}_{2}+2}$,
即ln[(1+ax1)(1+ax2)]>$\frac{2{x}_{1}({x}_{2}+2)+2{x}_{2}({x}_{1}+2)}{({x}_{1}+2)({x}_{2}+2)}$,
∴ln(1+a(x1+x2)+a2x1x2)>$\frac{4{x}_{1}{x}_{2}+4({x}_{1}+{x}_{2})}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$,
∵x1+x2=0,x1x2=$\frac{4a-4}{a}$,
∴ln(2a-1)2>$\frac{4(a-1)}{2a-1}$,
①2a-1>0,即$\frac{1}{2}<$a<1,则ln(2a-1)>$\frac{2a-2}{2a-1}$=1-$\frac{1}{2a-1}$.
令2a-1=t,则lnt+$\frac{1}{t}$-1>0,
设g(t)=lnt+$\frac{1}{t}$-1,则g′(t)=$\frac{1}{t}-\frac{1}{{t}^{2}}$=$\frac{t-1}{{t}^{2}}$,
∵$\frac{1}{2}$<a<1,∴0<t<1,∴g′(t)<0,
∴g(t)在(0,1)上是减函数,g(t)>g(1)=0,
∴lnt+$\frac{1}{t}$-1>0恒成立,∴$\frac{1}{2}<a<1$.
②若2a-1<0,即0$<a<\frac{1}{2}$,则ln(1-2a)>$\frac{2a-2}{2a-1}$=1+$\frac{1}{1-2a}$,
令1-2a=t,则lnt-$\frac{1}{t}$-1>0,
设h(t)=lnt-$\frac{1}{t}$-1,则h′(t)=$\frac{1}{t}+\frac{1}{{t}^{2}}$>0,
∵0$<a<\frac{1}{2}$,∴0<t<1,
∴h(t)在(0,1)上是增函数,∴h(t)<h(1)=-2,
∴lnt-$\frac{1}{t}$-1>0在(0,1)上无解.
综上,a的取值范围是($\frac{1}{2}$,1).
点评 本题考查了导数与函数单调性,极值的关系,函数单调性与不等式的解法,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | $C_n^{m-1}$ | B. | $A_n^{m-1}$ | C. | $C_n^m$ | D. | $A_n^m$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-2}{4}$ | B. | $\frac{π}{2}$-4 | C. | $\frac{π-1}{4}$ | D. | $\frac{π-4}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
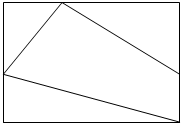 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$+3 | B. | $-2\sqrt{2}-3$ | C. | $2\sqrt{2}+3$ | D. | $2\sqrt{2}-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com