
分析 (1)求出抛物线的标准方程为x2=2y,由此能求出抛物线C的准线方程.
(2)P(x0,kx0-1),PQ的方程为y=$\frac{k{x}_{0}-2}{{x}_{0}-k}$(x-k)+1,与抛物线方程y=$\frac{1}{2}$x2联立,得x2-$\frac{2k{x}_{0}-4}{{x}_{0}-k}$x+$\frac{(2{k}^{2}-2){x}_{0}-2k}{{x}_{0}-k}$=0,由此利用韦达定理能证明|PM|•|ON|=|PN|•|QM|.
解答 解:(1)∵抛物线C:y=$\frac{1}{2}$x2,
∴抛物线的标准方程为x2=2y,
∴$\frac{p}{2}$=$\frac{1}{2}$,
∴抛物线C的准线方程为y=-$\frac{1}{2}$.
证明:(2)∵直线l:y=kx-1(k为常数),设点P为直线l上的动点,且P的横坐标为x0,Q(k,1)为定点,
∴P(x0,kx0-1),
PQ的方程为y=$\frac{k{x}_{0}-2}{{x}_{0}-k}$(x-k)+1,
与抛物线方程y=$\frac{1}{2}$x2联立,消去y,得
x2-$\frac{2k{x}_{0}-4}{{x}_{0}-k}$x+$\frac{(2{k}^{2}-2){x}_{0}-2k}{{x}_{0}-k}$=0
设M(x1,y1),N(x2,y2),则x1+x2=$\frac{2k{x}_{0}-4}{{x}_{0}-k}$,x1x2=$\frac{(2{k}^{2}-2){x}_{0}-2k}{{x}_{0}-k}$,①
要证|PM|•|ON|=|PN|•|QM|,只需证明2x1x2-(k+x0)(x3+x4)+2kx0=0,②
把①代入②:
2x1x2-(k+x0)(x3+x4)+2kx0
=$\frac{2(2{k}^{2}-2){x}_{0}-4k}{{x}_{0}-k}$-(x+x0)•$\frac{2k{x}_{0}-4}{{x}_{0}-k}$+2kx0
=$\frac{2(2{k}^{2}-2){x}_{0}-4k-(k+{x}_{0})(2k{x}_{0}-4)+2k{x}_{0}({x}_{0}-k)}{{x}_{0}-k}$=0,
∴|PM|•|ON|=|PN|•|QM|.
点评 本题考查抛物线的准线方程的求法,考查两组线段乘积相等的证明,是中档题,解题时要认真审题,注意抛物线性质、韦达定理的合理运用.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
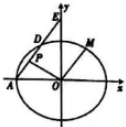 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1] | C. | (0,1) | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com