
| A. | [0,+∞) | B. | [0,1] | C. | (0,1) | D. | [0,1) |
分析 将函数两边平方,可得焦点在y轴上的双曲线的上支,由于双曲线的渐近线为y=±x,可得函数f(x)的图象上不同的两点连线的斜率范围为(-1,1),可得所求取值范围.
解答 解:∵$y=\sqrt{4+{x^2}}$,
∴两边平方可得,y2-x2=4(y>0),
∴函数$f(x)=\sqrt{4+{x^2}}$的图象表示焦点在y轴上的双曲线的上支,
由于双曲线的渐近线为y=±x,
所以函数f(x)的图象上不同的两点连线的斜率范围为(-1,1),
故$\frac{{|f({x_1})-f({x_2})|}}{{|{x_1}-{x_2}|}}∈[0,\;\;1)$,
故选:D.
点评 本题考查双曲线的图象和性质,注意运用渐近线与双曲线的关系,以及双曲线上两点的斜率和渐近线斜率的关系,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
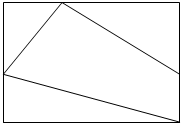 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充分必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$+3 | B. | $-2\sqrt{2}-3$ | C. | $2\sqrt{2}+3$ | D. | $2\sqrt{2}-3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com