
分析 (1)利用三角恒等变化化简函数的解析式,再利用正弦函数的周期性和单调性,得出结论.
(2)由f($\frac{A}{2}$)=2,求得A,再利用b+c=4以及基本不等式求得bc的范围,再利用余弦定理求得a的最小值.
解答 解:(1)∵函数f(x)=cos2x+2$\sqrt{3}$sinxcosx=cos2x+$\sqrt{3}$sin2x=2($\frac{1}{2}$cos2x+$\frac{\sqrt{3}}{2}$sin2x)=2sin(2x+$\frac{π}{6}$),
故函数f(x)的最小正周期为$\frac{2π}{2}$=π,
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,可得函数的增区间为[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],k∈Z.
(2)△ABC中,∵f($\frac{A}{2}$)=2sin(A+$\frac{π}{6}$)=2,∴A+$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,结合A+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{7π}{6}$),
可得A+$\frac{π}{6}$=$\frac{π}{2}$,∴A=$\frac{π}{3}$.
又b+c=4≥2$\sqrt{bc}$,∴0<bc≤4,
由 a2=b2+c2-2bc•cosA=(b+c)2-3bc=16-3bc∈[4,16),∴a∈[2,4),
综上可得,实数a的最小值为2.
点评 本题主要考查三角恒等变化,正弦函数的周期性和单调性,基本不等式的应用,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| 患心脏病 | 患其它病 | 合 计 | |
| 高血压 | 20 | 10 | 30 |
| 不高血压 | 30 | 50 | 80 |
| 合 计 | 50 | 60 | 110 |
| A. | 有99%以上的把握认为“高血压与患心脏病无关” | |
| B. | 有99%以上的把握认为“高血压与患心脏病有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
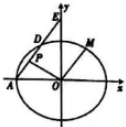 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{2\sqrt{2}}{3}$,经过椭圆的左顶点A(-3,0)作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴与点E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1] | C. | (0,1) | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com