
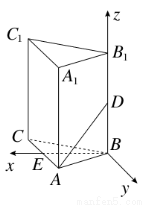
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为( )
A.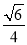 B.-
B.-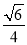 C.
C.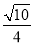 D.-
D.-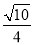
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
设e是椭圆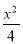 +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( )
A.(0,3) B.(3,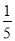 )
)
C.(0,3)∪(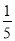 ,+∞) D.(0,2)
,+∞) D.(0,2)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:解答题
已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:解答题
设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:选择题
若直线l:y=kx-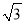 与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是( )
A.[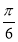 ,
,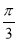 ) B.(
) B.(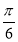 ,
,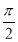 ) C.(
) C.(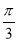 ,
,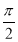 ) D.[
) D.[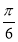 ,
,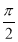 ]
]
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:填空题
已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是________.
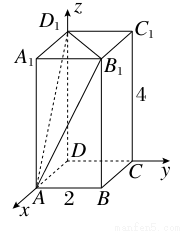
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
平面α经过三点A(-1,0,1),B(1,1,2),C(2,-1,0),则下列向量中与平面α的法向量不垂直的是( )
A.(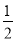 ,-1,-1) B.(6,-2,-2)
,-1,-1) B.(6,-2,-2)
C.(4,2,2) D.(-1,1,4)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-5直线、平面垂直的判定及性质(解析版) 题型:选择题
如图,在棱长为4的正四面体A-BCD中,M是BC的中点,点P在线段AM上运动(P不与A,M重合),过点P作直线l⊥平面ABC,l与平面BCD交于点Q,给出下列命题:①BC⊥平面AMD;②Q点一定在直线DM上;③VC-AMD=4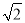 .
.
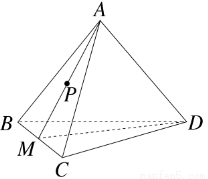
其中正确命题的序号是( )
A.①② B.①③ C.②③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-2空间几何体的表面积和体积(解析版) 题型:解答题
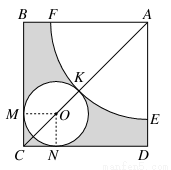
如图所示,在边长为5+ 的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
的长方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com