
已知定点M(0,2),N(-2,0),直线l:kx-y-2k+2=0(k为常数).
(1)若点M,N到直线l的距离相等,求实数k的值;
(2)对于l上任意一点P,∠MPN恒为锐角,求实数k的取值范围.
(1)k=1或k=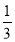
(2)k∈(-∞,-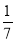 )∪(1,+∞)
)∪(1,+∞)
【解析】【解析】
(1)∵点M、N到直线l的距离相等,
∴直线l平行于MN所在的直线或过MN的中点,
∴k=1或k=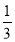 .
.
(2)设l上任意一点P(x0,kx0-2k+2).
若∠MPN恒为锐角,则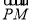 ·
·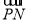 >0,
>0,
即(x0,kx0-2k)·(x0+2,kx0-2k+2)>0,
∴x02+2x0+(kx0-2k)2+2kx0-4k>0,
∴(1+k2)x02+(2k-4k2+2)x0+4k2-4k>0对x0∈R恒成立,
∴Δ=(2k-4k2+2)2-4(k2+1)(4k2-4k)<0,
即-7k2+6k+1<0,∴k>1或k<-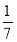 ,
,
即k∈(-∞,-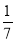 )∪(1,+∞).
)∪(1,+∞).


科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
已知点A(3,4),F是抛物线y2=8x的焦点,M是抛物线上的动点,当|AM|+|MF|最小时,M点坐标是( )
A.(0,0) B.(3,2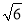 ) C.(2,4) D.(3,-2
) C.(2,4) D.(3,-2 )
)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:填空题
在平面直角坐标系xOy中,已知圆x2+y2=4上有且只有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:填空题
已知圆C过点A(1,0)和B(3,0),且圆心在直线y=x上,则圆C的标准方程为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-3圆的方程(解析版) 题型:选择题
设圆的方程是x2+y2+2ax+2y+(a-1)2=0,若0<a<1,则原点与圆的位置关系是( )
A.原点在圆上 B.原点在圆外
C.原点在圆内 D.不确定
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:填空题
若直线l1:x+2my-1=0与l2:(3m-1)x-my-1=0平行,则实数m的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-1直线的倾斜角与斜率、直线方程(解析版) 题型:解答题
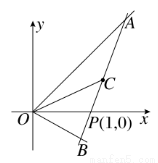
如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=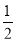 x上时,求直线AB的方程.
x上时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-7立体几何中的向量方法(解析版) 题型:选择题
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面AA1C1C所成的角的正弦值为( )
A.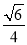 B.-
B.-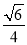 C.
C.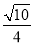 D.-
D.-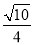
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:7-4直线、平面平行的判定及性质(解析版) 题型:解答题
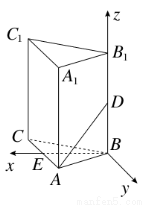
直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=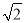 ,AA′=1,点M,N分别为A′B和B′C′的中点.
,AA′=1,点M,N分别为A′B和B′C′的中点.
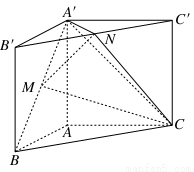
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′-MNC的体积.(锥体体积公式V=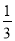 Sh,其中S为底面面积,h为高)
Sh,其中S为底面面积,h为高)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com