
分析 直接由数列递推式分段求出数列的前几项,可得数列{an}是周期为3的周期数列,则答案可求.
解答 解:由an+1=$\left\{\begin{array}{l}{2{a}_{n}(0≤{a}_{n}<\frac{1}{2})}\\{2{a}_{n}-1(\frac{1}{2}≤{a}_{n}<1)}\end{array}\right.$,且a1=$\frac{6}{7}$,得:
${a}_{2}=2{a}_{1}-1=2×\frac{6}{7}-1=\frac{5}{7}$,${a}_{3}=2{a}_{2}-1=2×\frac{5}{7}-1=\frac{3}{7}$,
${a}_{4}=2{a}_{3}=2×\frac{3}{7}=\frac{6}{7}$,${a}_{5}=2{a}_{4}-1=2×\frac{6}{7}-1=\frac{5}{7}$,…,
由上可知,数列{an}是周期为3的周期数列,
∴${a}_{2016}={a}_{3}=\frac{3}{7}$.
故答案为:$\frac{3}{7}$.
点评 本题考查数列递推式,考查了数列的函数特性,训练了分段函数的应用,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{π}{2}$] | B. | [$\frac{π}{2}$,π] | C. | [π,$\frac{3π}{2}$] | D. | [$\frac{3π}{2}$,2π] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a+b)<f(a) | B. | f(a+b)<f(a)+f(b) | C. | f(a+b)≤a+b | D. | f(a+b)>f(a)+f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (6,-10) | B. | (-6,10) | C. | (3,-5) | D. | (-3,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
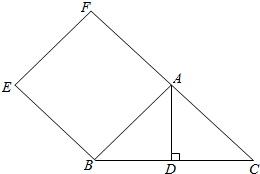 如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度.
如图,已知正方形ABEF的面积为10,以AB为直角边所作的等腰直角角形ABC的斜边BC=2$\sqrt{5}$,求BC边上的高AD的长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com