练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，正方体的棱长为，线段上有两个动点，且，则下列结论中正确的是（ ）

    A.

    B.平面

    C.与平面所成角是

    D.面积与的面积相等

    【答案】BC

    【解析】

    先连接，， 根据正方体结构特征，以及线面角的概念，线面垂直的判定定理等，逐项判断，即可得出结果.

    连接，，

    A选项，因为线段上的动点，若与重合，则在正方体中，，此时与所成的角为，显然与不垂直，故A错；

    B选项，因为正方体底面为正方形，对角线互相垂直，所以；又正方体侧棱与底面垂直，所以平面，所以，由线面垂直的判定定理，可得平面，又平面即为平面，所以平面；故B正确；

    C选项，由B选项可得，与平面所成角即为与平面所成角，即，

    所以在正方形中，；故C正确；

    D选项，因为点平面，点平面，由正方体结构特征易得，点到直线的距离大于正方体的侧棱长，而点到直线的距离等于侧棱长，因此面积与的面积不相等；故D错误；

    故选：BC.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是某地某月1日至15日的日平均温度变化的折线图，根据该折线图，下列结论正确的是（　　）

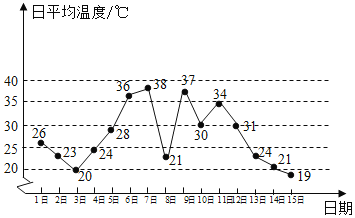
    A. 这15天日平均温度的极差为

    B. 连续三天日平均温度的方差最大的是7日，8日，9日三天

    C. 由折线图能预测16日温度要低于

    D. 由折线图能预测本月温度小于的天数少于温度大于的天数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知两点分别在轴和轴上运动，且，若动点

    满足，动点的轨迹为.

    （1）求的方程；

    （2）过点作动直线的平行线交轨迹于两点，则是否为定值？若是，求出该值；若不是，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有人认为在机动车驾驶技术上，男性优于女性.这是真的么？某社会调查机构与交警合作随机统计了经常开车的名驾驶员最近三个月内是否有交通事故或交通违法事件发生，得到下面的列联表：

    男

    女

    合计

    无

    40

    35

    75

    有

    15

    10

    25

    合计

    55

    45

    100

    附：.

    0.50

    0.40

    0.25

    0.15

    0.10

    0.455

    0.708

    1.323

    2.072

    2.706

    据此表，可得

    A. 认为机动车驾驶技术与性别有关的可靠性不足

    B. 认为机动车驾驶技术与性别有关的可靠性超过

    C. 认为机动车驾驶技术与性别有关的可靠性不足

    D. 认为机动车驾驶技术与性别有关的可靠性超过

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，已知抛物线的焦点F在y轴上，其准线与双曲线的下准线重合．

    （1）求抛物线的标准方程；

    （2）设A(，)(＞0)是抛物线上一点，且AF＝，B是抛物线的准线与y轴的交点．过点A作抛物线的切线l，过点B作l的平行线l′，直线l′与抛物线交于点M，N，求△AMN的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥中，平面，， 是线段的中垂线， ，为线段上的点．

    （Ⅰ）证明：平面平面；

    （Ⅱ）若为的中点，求异面直线与所成角的正切值；

    （Ⅲ）求直线与平面所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的方程为，离心率为，它的一个顶点恰好是抛物线的焦点.

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）过动点的直线交轴的负半轴于点，交C于点(在第一象限)，且是线段的中点，过点作x轴的垂线交C于另一点，延长线交C于点.

    (i)设直线，的斜率分别为，，证明：；

    (ii)求直线的斜率的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查，对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分，其评分情况如下表所示：

    中学编号

    1

    2

    3

    4

    5

    6

    7

    8

    原料采购加工标准评分x

    100

    95

    93

    83

    82

    75

    70

    66

    卫生标准评分y

    87

    84

    83

    82

    81

    79

    77

    75

    （1）已知x与y之间具有线性相关关系，求y关于x的线性回归方程；（精确到0.1）

    （2）现从8个被检查的中学食堂中任意抽取两个组成一组，若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分，则组成“对比标兵食堂”，求该组被评为“对比标兵食堂”的概率.

    参考公式：，；

    参考数据：，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点为椭圆上任意一点，直线与圆交于两点，点为椭圆的左焦点．

    （Ⅰ）求椭圆的离心率及左焦点的坐标；

    （Ⅱ）求证：直线与椭圆相切；

    （Ⅲ）判断是否为定值，并说明理由．

    查看答案和解析>>

    同步练习册答案