
分析 (1)椭圆的中心为坐标原点O,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,且过点B(0,1),求出a,b,由此能求出椭圆方程.
(2)由平几知|ON|2=|OK||OM|,直线OM:y=$\frac{t}{2}$x,直线FN:y=-$\frac{2}{t}$(x-1),联立得xK=$\frac{4}{{t}^{2}+4}$.由此能证明线段ON的长为定值.
(3)利用椭圆的参数方程,即可得出结论.
解答 (1)解:∵椭圆的中心为坐标原点O,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,且过点B(0,1),
∴b=1,$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,从而a=$\sqrt{2}$.…(2分)
∴椭圆方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$.…(4分)
(2)证明:由平几知:|ON|2=|OK||OM|,(K为垂足)
直线OM:y=$\frac{t}{2}$x,直线FN:y=-$\frac{2}{t}$(x-1),联立得xK=$\frac{4}{{t}^{2}+4}$.
∴|ON|2=$\sqrt{(1+\frac{{t}^{2}}{4}){x}_{K}}$•$\sqrt{(1+\frac{{t}^{2}}{4}){x}_{M}}$=(1+$\frac{{t}^{2}}{4}$)•$\frac{4}{{t}^{2}+4}$•2=2.
∴线段ON的长为定值$\sqrt{2}$. …(8分)
(3)解:设x=$\sqrt{2}$cosα,y=sinα,则x+y=$\sqrt{2}$cosα+sinα=$\sqrt{3}$sin(α+θ),
∴x+y的最大、最小值分别为$\sqrt{3}$,-$\sqrt{3}$. …(12分)
点评 本题考查椭圆的方程与运用,考察平面几何知识,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
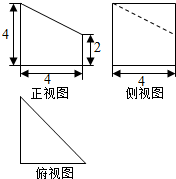
| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{80}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x-a|≤3a | B. | |x-a|<3a | C. | |x-a|<0.03a | D. | |x-a|≤0.03a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {1} | C. | [-2,0] | D. | {-2,-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
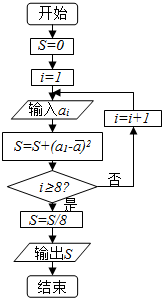 对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:
对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 100 | 101 | 103 | 103 | 104 | 106 | 107 | 108 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com