
分析 (1)先将函数化为y=Asin(ωx+φ)的形式,将内层函数看作整体,放到正弦函数的增区间上,解不等式得函数的单调递增区间;
(2)根据(1)得f(x)的解析式,求出C角,在根据平面向量共线的特征,建立角A,B的关系式,利用余弦定理即可求a,b的值.
解答 解:由f(x)=$\frac{\sqrt{3}}{2}$sin2x-cos2x-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}-\frac{1}{2}cos2x$-$\frac{1}{2}$
=$\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x-1$
=sin$(2x-\frac{π}{6})$-1,
根据正弦函数图象及性质可得:$2x-\frac{π}{6}∈$[2kπ-$\frac{π}{2}$,2kπ$+\frac{π}{2}$](k∈Z)是增区间.
即2kπ-$\frac{π}{2}$≤$2x-\frac{π}{6}$≤2kπ$+\frac{π}{2}$,解得:$-\frac{π}{6}+kπ$≤x≤$\frac{π}{3}+kπ$.
∴f(x)的单调增区间为[$-\frac{π}{6}+kπ$,$\frac{π}{3}+kπ$]](k∈Z).
(2)由(1可知)f(x)=sin$(2x-\frac{π}{6})$-1
∴f(C)=sin$(2C-\frac{π}{6})-1$
又f(C)=0,即sin$(2C-\frac{π}{6})-1$=0.
解得:C=$\frac{π}{3}$.
由题意:向量$\overrightarrow{m}$=(1,sinA)与向量$\overrightarrow{n}$=(2,sinB)共线,
则有:sinB-2sinA=0
∴$\frac{1}{2}=\frac{sinA}{sinB}$
由正弦定理可得:b=2a…①
由余弦定理$cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$
可得:$\frac{1}{2}=\frac{{a}^{2}+{b}^{2}-3}{2ab}$
化简:a2+b2-ab=3…②
由①②解得:a=1,b=2.
点评 本题考查了三角函数的图象和性质的运用,向量的共线问题和正、余弦定理的化简以及计算能力.属于中档题.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 22 | C. | 24 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
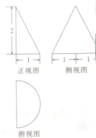
| A. | π | B. | 2+$\frac{1+\sqrt{5}}{2}π$ | C. | 2+$\frac{2+\sqrt{5}}{2}$π | D. | 2+$\frac{1}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com