
命题:“若空间两条直线a,b分别垂直平面α,则a∥b”,学生小夏这样证明:
设a,b与平面α分别相交于A,B,连接AB,
∵a⊥α,b⊥α,AB⊂α,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,即:
①⇒②和②⇒③,老师认为小夏的推理证明不正确,这两个推理中不正确的是 .
科目:高中数学 来源: 题型:
如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点.

(1)求证A,I,H,E四点共圆;
(2)若∠C=50°,求∠IEH的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤ 对一切x∈R恒成立,则
对一切x∈R恒成立,则
①f =0;
=0;
②︱f ︱<︱f
︱<︱f ︱;
︱;
③f(x)既不是奇函数也不是偶函数;
④f(x)的单调递增区间是[kπ+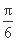 ,kπ+
,kπ+ ](k∈Z);
](k∈Z);
⑤存在经过点(a,b)的直线与函数f(x)的图象不相交.
以上结论正确的是 (写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则cos∠F1PF2=( )
(A)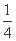 (B)
(B)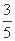 (C)
(C)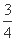 (D)
(D)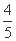
查看答案和解析>>
科目:高中数学 来源: 题型:
若点P是以A(- ,0),B(
,0),B( ,0)为焦点,实轴长为2
,0)为焦点,实轴长为2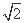 的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )
的双曲线与圆x2+y2=10的一个交点,则|PA|+|PB|的值为( )
(A)2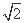 (B)4
(B)4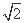 (C)4
(C)4 (D)6
(D)6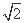
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com