
函数y=sin2x+sin x-1的值域为( )
(A)[-1,1] (B)[-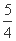 ,-1]
,-1]
(C)[-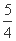 ,1] (D)[-1,
,1] (D)[-1,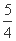 ]
]
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知点A(4,4)在抛物线y2=px(p>0)上,该抛物线的焦点为F,过点A作直线l:x=- 的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
的垂线,垂足为M,则∠MAF的平分线所在直线的方程为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,AB为☉O直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明:

(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
函数y=f(x)在(0,2)上是增函数,函数y=f(x+2)是偶函数,则f(1),f(2.5),f(3.5)的大小关系是( )
(A)f(2.5)<f(1)<f(3.5)
(B)f(2.5)>f(1)>f(3.5)
(C)f(3.5)>f(2.5)>f(1)
(D)f(1)>f(3.5)>f(2.5)
查看答案和解析>>
科目:高中数学 来源: 题型:
命题:“若空间两条直线a,b分别垂直平面α,则a∥b”,学生小夏这样证明:
设a,b与平面α分别相交于A,B,连接AB,
∵a⊥α,b⊥α,AB⊂α,①
∴a⊥AB,b⊥AB,②
∴a∥b.③
这里的证明有两个推理,即:
①⇒②和②⇒③,老师认为小夏的推理证明不正确,这两个推理中不正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=Asin(ωx+)(其中A>0,ω>0,-π<≤π)在x=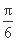 处取得最大值2,其图象与x轴的相邻两个交点的距离为
处取得最大值2,其图象与x轴的相邻两个交点的距离为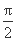 .
.
(1)求f(x)的解析式;
(2)求函数g(x)= 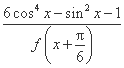 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
设圆锥曲线C的两个焦点分别为F1、F2,若曲线C上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线C的离心率等于( )
(A) 或
或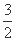 (B)
(B) 或2
或2
(C)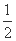 或2 (D)
或2 (D)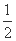 或
或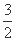
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com