
 某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的AB,DC)和两个半圆构成,设AB=xm,且x≥80.
某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的AB,DC)和两个半圆构成,设AB=xm,且x≥80.分析 (1)设半圆的半径为r,可得x+πr=200,矩形ABCD的面积为S=2xr=$\frac{2}{π}$x•πr,运用基本不等式即可得到所求最小值及x的值;
(2)设半圆的半径为r,由题意可得2x=$\frac{22500}{πr}$-πr,即有内圈周长c=2x+2πr=$\frac{22500}{πr}$+πr,由x≥80,求得r的范围,设出f(r)=$\frac{22500}{πr}$+πr,求得导数,判断单调性,即可得到所求最小值及x的值.
解答 解:(1)设半圆的半径为r,
可得2x+2πr=400,即x+πr=200,
矩形ABCD的面积为S=2xr=$\frac{2}{π}$x•πr≤$\frac{2}{π}$•($\frac{x+πr}{2}$)2=$\frac{20000}{π}$,
当且仅当x=πr=100m时,矩形的面积取得最大值$\frac{20000}{π}$m2;
(2)设半圆的半径为r,
由题意可得πr2+2xr=$\frac{22500}{π}$,可得2x=$\frac{22500}{πr}$-πr,
即有内圈周长c=2x+2πr=$\frac{22500}{πr}$+πr,
由x≥80,可得$\frac{22500}{πr}$-πr≥160,
解得0<πr≤90,
可得f(r)=$\frac{22500}{πr}$+πr,f′(r)=π-$\frac{22500}{π{r}^{2}}$,
即有f(r)在(0,$\frac{90}{π}$]上递减,
即有πr=90,即x=80m时,周长c取得最小值340m.
点评 本题考查函数的应用题的解法,考查最值的求法,注意运用基本不等式和函数的单调性,正确理解题意和点到函数式是解题的关键.


科目:高中数学 来源: 题型:选择题
| A. | {x∈R|1≤x<2} | B. | {x∈R|x<1} | C. | {x∈R|2<x≤5} | D. | {x∈R|2≤x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {3.4} | C. | {3.4,5} | D. | {3.4,5,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
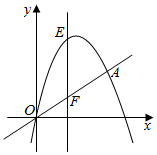 如图所示,已知二次函数y=-x2+4x+c的图象经过坐标原点,并且与函数y=x的图象交于O,A两点.求:
如图所示,已知二次函数y=-x2+4x+c的图象经过坐标原点,并且与函数y=x的图象交于O,A两点.求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com