
【题目】设向量 ![]() ,
, ![]() ,
, ![]() 满足|
满足| ![]() |=2,|
|=2,| ![]() +
+ ![]() |=6,|
|=6,| ![]() |=|
|=| ![]() |,且
|,且 ![]() ⊥
⊥ ![]() ,则|
,则| ![]() ﹣
﹣ ![]() |的取值范围为( )
|的取值范围为( )
A.[4,8]
B.[4 ![]() ,8
,8 ![]() ]
]
C.(4,8)
D.(4 ![]() ,8
,8 ![]() )
)
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上且以2为周期的偶函数,当0≤x≤1,f(x)=x2 . 如果函数g(x)=f(x)﹣(x+m)有两个零点,则实数m的值为( )
A.2k(k∈Z)
B.2k或2k+ ![]() (k∈Z)
(k∈Z)
C.0
D.2k或2k﹣ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1= ![]() ,2Sn﹣SnSn﹣1=1(n≥2).
,2Sn﹣SnSn﹣1=1(n≥2).
(1)求S1 , S2 , S3 , S4并猜想Sn的表达式(不必写出证明过程);
(2)设bn= ![]() ,n∈N*,求bn的最大值.
,n∈N*,求bn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥V﹣ABC中,VA=VB=AC=BC=2,AB=2 ![]() ,VC=1,线段AB的中点为D.
,VC=1,线段AB的中点为D.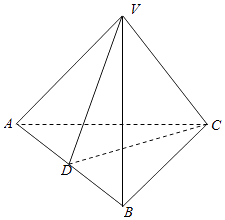
(1)求证:平面VCD⊥平面ABC;
(2)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(1)已知点H(x0 , y0)在圆C:x2+y2+Dx+Ey+F=0(其中点C为圆心,D2+E2﹣4F>0)外,由点H向圆C引切线,其中一个切点为M.
求证:|HM|= ![]() ;
;
(2)如图,P是直线x=4上一动点,以P为圆心的圆P经定点B(1,0),直线l是圆P在点B处的切线,过A(﹣1,0)作圆P的两条切线分别与l交于E,F两点.
求证:|EA|+|EB|为定值.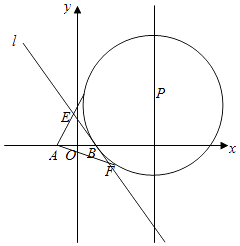
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,Sn=2n2+5n.
(1)求证:数列{3 ![]() }为等比数列;
}为等比数列;
(2)设bn=2Sn﹣3n,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{cn}的前n项和,an=2n , bn=50﹣3n,cn= ![]() .
.
(1)求c4与c8的等差中项;
(2)当n>5时,设数列{Sn}的前n项和为Tn .
(ⅰ)求Tn;
(ⅱ)当n>5时,判断数列{Tn﹣34ln}的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )
x3﹣(a﹣1)x2+b2x,其中a∈{1,2,3,4},b∈{1,2,3},则函数f(x)在R上是增函数的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com