
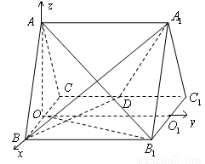
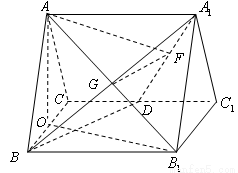
如图,三棱柱 侧棱与底面垂直,且所有棱长都为4,D为CC1中点.
侧棱与底面垂直,且所有棱长都为4,D为CC1中点.

(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)见解析;(2)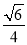 .
.
【解析】
试题分析:取BC中点O,连AO,利用正三角形三线合一,及面面垂直的性质可得AO⊥平面BCB1C1,取B1C1中点为O1,以O为原点,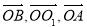 的方向为x,y,z轴的正方向,建立空间直角坐标系,
的方向为x,y,z轴的正方向,建立空间直角坐标系,
(1)求出AB1的方向向量 利用向量垂直的充要条件及线面垂直的判定定理可得AB1⊥平面A1BD;
利用向量垂直的充要条件及线面垂直的判定定理可得AB1⊥平面A1BD;
(2)分别求出平面A1AD的法向量和平面A1AD的一个法向量代入向量夹角公式,可得二面角A-A1D-B的余弦值大小.也可用传统几何方法解决.
试题解析:法一:(向量法)
(1)取 中点
中点 ,连结
,连结 .取
.取 中点
中点 ,
,


 故:以
故:以 为原点,以
为原点,以 分别为
分别为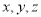 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 . 2分
. 2分
则: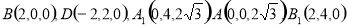 3分
3分
 4分
4分
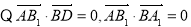 ,
, . 6分
. 6分
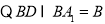
 平面
平面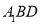 . 7分
. 7分
(2)设平面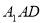 的法向量为
的法向量为 .
. .
.
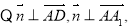

令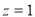 得
得 为平面
为平面 的一个法向量. 10分
的一个法向量. 10分
由(1)可知: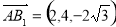 为平面
为平面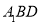 的法向量. 11分
的法向量. 11分
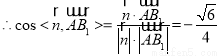 . 13分
. 13分
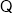 二面角
二面角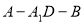 是锐角
是锐角  二面角
二面角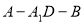 的余弦值为为
的余弦值为为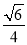 . 14分
. 14分
法二:(传统几何法)
(1)取BC中点O,连结AO和 ,
,


 2分
2分
 3分
3分
在正方形 中,
中,
 分别为
分别为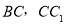 的中点,
的中点,
由正方形性质知: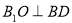 , 4分
, 4分
 5分
5分
又在正方形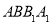 中,
中,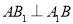 , 6分
, 6分
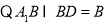
 平面
平面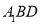 . 7分
. 7分
(2)设AB1与A1B交于点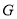 ,在平面
,在平面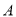 1BD中,作
1BD中,作 于
于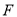 ,连结
,连结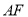 ,
,
由(1)得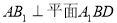 .
. 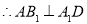

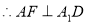
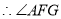 为二面角
为二面角 的平面角. 10分
的平面角. 10分
在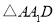 中,由等面积法可求得
中,由等面积法可求得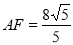 , 12分
, 12分
又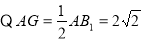 ,
, 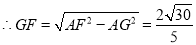 13分
13分
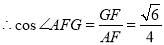 . 所以二面角
. 所以二面角 的余弦值为
的余弦值为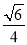 . 14分
. 14分
考点:1.二面角的平面角及求法;2.直线与平面垂直的判定.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届江苏省苏州市高三上学期期中测试数学试卷(解析版) 题型:解答题
(本小题满分10分)某校要进行特色学校评估验收,有甲、乙、丙、丁、戊五位评估员将随机去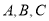 三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
三个不同的班级进行随班听课,要求每个班级至少有一位评估员.
(1)求甲、乙同时去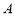 班听课的概率;
班听课的概率;
(2)设随机变量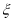 为这五名评估员去
为这五名评估员去 班听课的人数,求
班听课的人数,求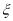 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考理科数学试卷(解析版) 题型:选择题
在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务. 已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处.则不同的搜寻方案有( )
A.40种 B.70种 C.80种 D.100种
查看答案和解析>>
科目:高中数学 来源:2015届广东省深圳市高三上学期第一次五校联考文科数学试卷(解析版) 题型:选择题
已知函数 是定义在R上的奇函数,
是定义在R上的奇函数,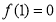 ,当
,当 时,有
时,有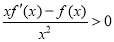 成立,则不等式
成立,则不等式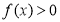 的解集是
的解集是
A.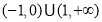 B.
B.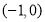 C.
C.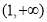 D.
D.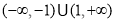
查看答案和解析>>
科目:高中数学 来源:2015届广东省高三上学期暑假联考文科数学试卷(解析版) 题型:填空题
从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com